Degenerate parabolic equation
From Encyclopedia of Mathematics
A partial differential equation
 |
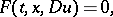where the function 
has the following property: For some even natural number 
, all roots 
of the polynomial
 |
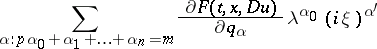have non-positive real parts for all real 
and, for certain 
, 
, 
, and 
, 
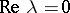for some root 
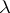, or for certain 
, 
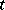and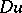 
the leading coefficient at 
vanishes. Here 
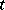is an independent variable which is often interpreted as time; 
is an 
-dimensional vector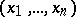 
; 
is the unknown function;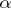 
is a multi-index 
; 
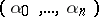is the vector with components
 |
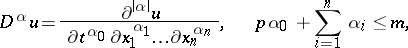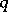is a vector with components 
, 
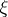is an 
-dimensional vector 
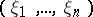, and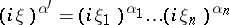 
. See also Degenerate partial differential equation, and the references given there.
How to Cite This Entry:
Degenerate parabolic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_parabolic_equation&oldid=18826
Degenerate parabolic equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_parabolic_equation&oldid=18826
This article was adapted from an original article by A.M. Il'in (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article