Favard problem

The problem of calculating the least upper bound

(*)

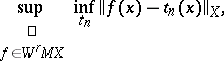where the are trigonometric polynomials of order not exceeding , is the class of periodic functions whose -th derivative in the sense of Weyl (see Fractional integration and differentiation) satisfies the inequality , and . The Favard problem was posed by J. Favard [1]. Subsequently, broader classes of functions have been considered and a complete solution of the Favard problem for and arbitrary has been obtained as a corollary of more general results (see [2], [3]).

References

[1]	J. Favard, "Sur les meilleurs procédés d'approximation de certaines classes de fonctions par des polynômes trigonométriques" Bull. Sci. Math. , 61 (1937) pp. 209–224
[2]	S.B. Stechkin, "On best approximation of certain classes of periodic functions by trigonometric functions" Izv. Akad. Nauk SSSR Ser. Mat. , 20 : 5 (1956) pp. 643–648 (In Russian)
[3]	V.K. Dzyadyk, "Best approximation on classes of periodic functions defined by kernels which are integrals of absolutely monotone functions" Izv. Akad. Nauk SSSR Ser. Mat. , 23 : 6 (1959) pp. 933–950 (In Russian)
[4]	N.P. Korneichuk, "Extremal problems in approximation theory" , Moscow (1976) (In Russian)

References

[a1]	R.P. Feinerman, D.J. Newman, "Polynomial approximation" , Williams & Wilkins pp. Chapt. IV.4