System (in a category)
direct and inverse system in a category 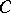
A direct system 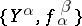 in
in 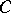 consists of a collection of objects
consists of a collection of objects 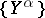 , indexed by a directed set
, indexed by a directed set  , and a collection of morphisms
, and a collection of morphisms 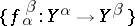 in
in 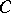 , for
, for 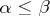 in
in 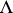 , such that
, such that
a)  for
for 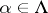 ;
;
b) 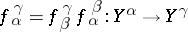 for
for  in
in 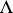 .
.
There exists a category, 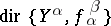 , whose objects are indexed collections of morphisms
, whose objects are indexed collections of morphisms  such that
such that 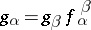 if
if 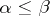 in
in 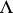 and whose morphisms with domain
and whose morphisms with domain 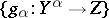 and range
and range 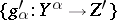 are morphisms
are morphisms 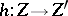 such that
such that 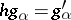 for
for 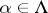 . An initial object of
. An initial object of 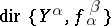 is called a direct limit of the direct system
is called a direct limit of the direct system 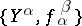 . The direct limits of sets, topological spaces, groups, and
. The direct limits of sets, topological spaces, groups, and 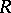 -modules are examples of direct limits in their respective categories.
-modules are examples of direct limits in their respective categories.
Dually, an inverse system 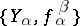 in
in 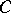 consists of a collection of objects
consists of a collection of objects 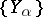 , indexed by a directed set
, indexed by a directed set  , and a collection of morphisms
, and a collection of morphisms 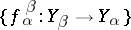 in
in 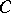 , for
, for  in
in 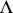 , such that
, such that
a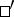 )
) 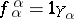 for
for 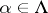 ;
;
b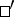 )
) 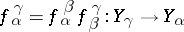 for
for  in
in 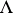 .
.
There exists a category,  , whose objects are indexed collections of morphisms
, whose objects are indexed collections of morphisms  such that
such that  if
if 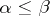 in
in 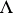 and whose morphisms with domain
and whose morphisms with domain 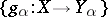 and range
and range 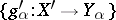 are morphisms
are morphisms 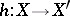 of
of 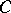 such that
such that 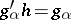 for
for 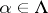 . A terminal object of
. A terminal object of 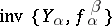 is called an inverse limit of the inverse system
is called an inverse limit of the inverse system 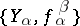 . The inverse limits of sets, topological spaces, groups, and
. The inverse limits of sets, topological spaces, groups, and 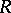 -modules are examples of inverse limits in their respective categories.
-modules are examples of inverse limits in their respective categories.
The concept of an inverse limit is a categorical generalization of the topological concept of a projective limit.
References
| [1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
Comments
There is a competing terminology, with "direct limit" replaced by "colimit" , and "inverse limit" by "limit" .
References
| [1a] | B. Mitchell, "Theory of categories" , Acad. Press (1965) |
System (in a category). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=System_(in_a_category)&oldid=18745