Voronoi summation method
A matrix summation method of sequences. It is defined by a numerical sequence 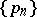 and denoted by the symbol
and denoted by the symbol 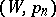 . A sequence
. A sequence 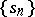 is summable by the method
is summable by the method 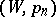 to a number
to a number 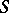 if
if
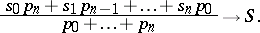 |
In particular, if 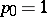 ,
, 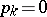 ,
, 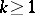 , the summability of a sequence by the
, the summability of a sequence by the 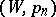 -method to a number
-method to a number 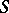 means that the sequence converges to
means that the sequence converges to 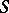 . For
. For 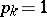 ,
, 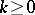 , one obtains the Cesàro summation method (cf. Cesàro summation methods). For
, one obtains the Cesàro summation method (cf. Cesàro summation methods). For 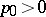 ,
, 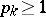 ,
, 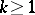 , the
, the 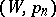 -method is regular (cf. Regular summation methods) if and only if
-method is regular (cf. Regular summation methods) if and only if 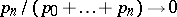 . Any two regular methods
. Any two regular methods 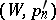 and
and 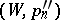 are compatible (cf. Compatibility of summation methods).
are compatible (cf. Compatibility of summation methods).
The Voronoi summation method was first introduced by G.F. Voronoi [1] and was rediscovered by N.E. Nörlund in 1919. The method is therefore sometimes referred to in western literature as the Nörlund method and the symbol given to it is 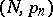 or
or 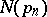 .
.
References
| [1] | G.F. [G.F. Voronoi] Woronoi, "Extension of the notion of the limit of the sum of terms of an infinite series" Ann. of Math. (2) , 33 (1932) pp. 422–428 ((With notes by J.D. Tamarkin.)) |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
Comments
References
| [a1] | C.N. Moore, "Summable series and convergence factors" , Dover, reprint (1966) |
Voronoi summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Voronoi_summation_method&oldid=18737