Whitehead multiplication

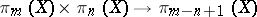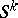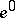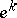A multiplication in homotopy groups , defined by G.W. Whitehead . In one takes a fixed decomposition into two cells and . Then the product of spheres 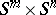has a decomposition into cells 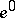, , 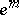, 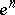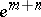. Therefore the characteristic mapping :

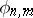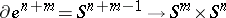factorizes as

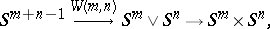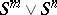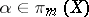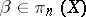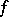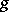where is a bouquet of spheres. Now, take classes and , represented by mappings and . Then the Whitehead product 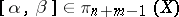is given by the composition

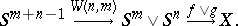The following properties are satisfied by this product:

1) ;

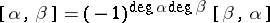2) if 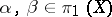, then ;

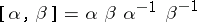3) if 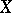is -simple, then 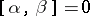for , ;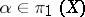

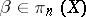4) if 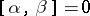for all 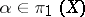, , 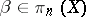then 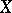is -simple;

5) if 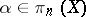, , 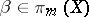, , 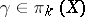then

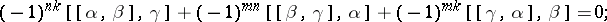6) the element 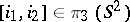, where 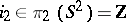is a generator, is equal to twice the generator of ;

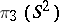7) the kernel of the epimorphism is generated by one element, 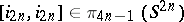, where 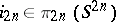is the canonical generator.

References

[1a]	G.W. Whitehead, "On products in homotopy groups" Ann. of Math. , 47 (1946) pp. 460–475
[1b]	G.W. Whitehead, "A generalization of the Hopf invariant" Ann. of Math. , 51 (1950) pp. 192–237

References

[a1]	G.W. Whitehead, "Elements of homotopy theory" , Springer (1978)
[a2]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. 419–420
[a3]	S.-T. Hu, "Homotopy theory" , Acad. Press (1959) pp. 138–139