Channel with a finite number of states
finite-state channel
A communication channel for which the statistical properties of the output signal at a time  are determined by the input signal at this moment and the state of the channel at the previous moment, and where the set of possible states of the channel is finite. A channel with a finite number of states can also be defined by a finite probabilistic automaton (cf. Automaton, probabilistic). Below a rigorous definition is given of a discrete-time homogeneous channel with a finite number of states and with finite spaces of values,
are determined by the input signal at this moment and the state of the channel at the previous moment, and where the set of possible states of the channel is finite. A channel with a finite number of states can also be defined by a finite probabilistic automaton (cf. Automaton, probabilistic). Below a rigorous definition is given of a discrete-time homogeneous channel with a finite number of states and with finite spaces of values, 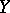 and
and 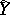 , for the components of the input and output signals. Suppose that functions
, for the components of the input and output signals. Suppose that functions 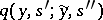 ,
, 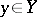 ,
, 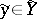 ,
, 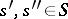 , are given, where
, are given, where 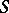 is a finite set, called the set of states of the channel, as well as a probability distribution
is a finite set, called the set of states of the channel, as well as a probability distribution 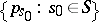 . Intuitively, the function
. Intuitively, the function 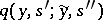 defines the conditional probability that at a time
defines the conditional probability that at a time 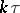 the signal
the signal  appears at the output and the channel goes over to the state
appears at the output and the channel goes over to the state 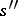 under the condition that the signal
under the condition that the signal 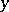 was transmitted and that at the previous moment
was transmitted and that at the previous moment 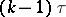 the channel was in state
the channel was in state  . The distribution
. The distribution  can be regarded as the probability distribution of the initial state of the channel (that is, the state of the channel at the initial moment). Let the functions
can be regarded as the probability distribution of the initial state of the channel (that is, the state of the channel at the initial moment). Let the functions 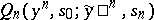 be recursively defined by the formulas
be recursively defined by the formulas
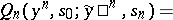 |
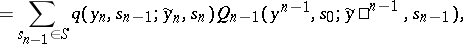 |
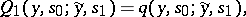 |
where 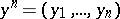 ,
, 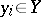 ,
, 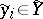 ,
, 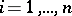 ,
, 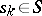 ,
, 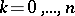 . Let
. Let
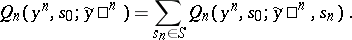 |
Then the transition function
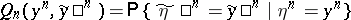 |
of segments of length  of the channel with a finite number of states, for any
of the channel with a finite number of states, for any  , is, by definition, equal to
, is, by definition, equal to
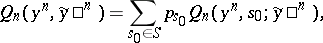 |
where 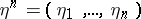 and
and 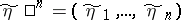 are the segments of length
are the segments of length  of the input and the output of the channel.
of the input and the output of the channel.
For references see ,
in the article Communication channel.
Channel with a finite number of states. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Channel_with_a_finite_number_of_states&oldid=18715