Semi-linear mapping

A mapping 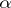from a (left) module 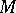into a (left) module 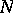over the same ring 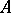, satisfying the conditions

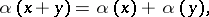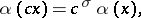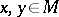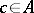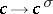where , and is some automorphism of 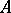. One says that 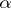is semi-linear relative to the automorphism 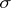. A semi-linear mapping of vector spaces over the field 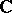relative to complex conjugation 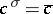is also known as an anti-linear mapping. A semi-linear mapping of an 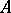-module 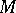into itself is known as a semi-linear transformation.

Example. A homothety of an -module , i.e. a mapping 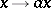(), where is a fixed invertible element of 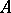, is a semi-linear mapping relative to the automorphism .

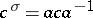Many properties of linear mappings and homomorphisms of modules remain valid for semi-linear mappings. In particular, the kernel and image of a semi-linear mapping are submodules; semi-linear mappings of free modules with finite bases are completely determined by their matrices; one can define the rank of a semi-linear mapping of vector spaces, which is equal to the rank of its matrix; etc.

References

[1]	N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Addison-Wesley (1973) pp. Chapts. I-III (Translated from French)

Comments

A semi-linear transformation, i.e. a semi-linear mapping of a module into itself, is also called a semi-linear endomorphism.