Group object
of a category
An object 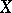 of a category
of a category 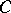 such that for any
such that for any 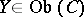 the set of morphisms
the set of morphisms 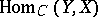 is a group, while the correspondence
is a group, while the correspondence  is a functor from
is a functor from 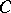 into the category of groups Gr. A homomorphism of a group object
into the category of groups Gr. A homomorphism of a group object  into a group object
into a group object 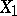 is a morphism
is a morphism 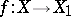 of
of 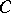 such that for any
such that for any 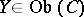 the corresponding mapping
the corresponding mapping 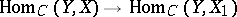 is a homomorphism of groups. The group objects of a category
is a homomorphism of groups. The group objects of a category 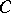 and homomorphisms between them form the category
and homomorphisms between them form the category  . The functor
. The functor 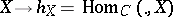 establishes an equivalence between the category
establishes an equivalence between the category 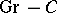 and the category of representable pre-sheaves of groups on
and the category of representable pre-sheaves of groups on 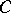 . If the values of the functor
. If the values of the functor 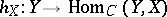 belong to the subcategory Ab of Abelian groups, then the group object
belong to the subcategory Ab of Abelian groups, then the group object 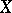 is said to be commutative or Abelian. If
is said to be commutative or Abelian. If 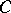 has finite products and a final object
has finite products and a final object  , a group object
, a group object 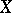 of
of 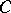 is defined by the following properties.
is defined by the following properties.
There exist morphisms 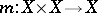 (multiplication),
(multiplication), 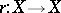 (inversion) and
(inversion) and 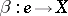 (a unit) satisfying the following axioms.
(a unit) satisfying the following axioms.
Associativity. The diagram
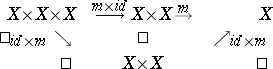 |
is commutative.
Existence of a unit element. The diagram
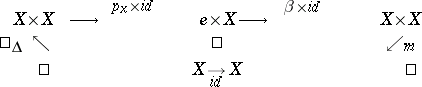 |
is commutative.
Existence of an inverse element. The diagram
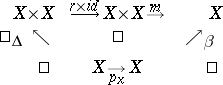 |
is commutative. Here 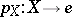 is the canonical morphism of
is the canonical morphism of 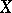 into the final object
into the final object  , while
, while 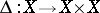 is the diagonal morphism.
is the diagonal morphism.
If 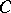 is the category of sets Ens, group objects are precisely groups. The final object of the category Ens is the set
is the category of sets Ens, group objects are precisely groups. The final object of the category Ens is the set 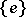 consisting of the single element
consisting of the single element  . Axiom a) denotes the associativity of the binary operation given by the morphism
. Axiom a) denotes the associativity of the binary operation given by the morphism 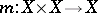 . The morphism
. The morphism 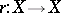 is the mapping of inversion, while the morphism
is the mapping of inversion, while the morphism 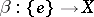 is the mapping of the set
is the mapping of the set 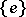 into
into 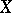 , whose image is equal to the unit element in
, whose image is equal to the unit element in 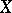 .
.
In a similar manner it is possible to define a ring object of a category and, generally, to specify an algebraic structure on an object of a category [2].
References
| [1] | Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" Russian Math. Surveys , 18 (1963) pp. 1–80 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 3–90 |
| [2] | M. Demazure, A. Grothendieck, "Schémas en groupes I" , Lect. notes in math. , 151–153 , Springer (1970) |
Comments
Group objects, in particular categories, are often objects of interest in their own right. For example, topological groups (cf. Topological group) are group objects in the category of topological spaces and continuous mappings; Lie groups (cf. Lie group) are group objects in the category of smooth manifolds; and sheaves of groups on a given space 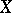 are group objects in the category of sheaves of sets on
are group objects in the category of sheaves of sets on 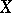 . A group object in a category of the form
. A group object in a category of the form 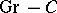 is an object of
is an object of  equipped with two commuting group structures; it is easily seen that in this case the two structures must coincide and be Abelian, and conversely an Abelian group structure commutes with itself, so that
equipped with two commuting group structures; it is easily seen that in this case the two structures must coincide and be Abelian, and conversely an Abelian group structure commutes with itself, so that 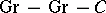 is isomorphic to the category
is isomorphic to the category 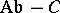 of Abelian group objects in
of Abelian group objects in 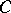 . A functor which preserves finite products (including the final object) preserves group objects; using this and the above identification, one obtains an easy proof of the result that the fundamental group of a topological group is Abelian.
. A functor which preserves finite products (including the final object) preserves group objects; using this and the above identification, one obtains an easy proof of the result that the fundamental group of a topological group is Abelian.
References
| [a1] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7 |
| [a2] | B. Eckmann, P.J. Hilton, "Group-like structures in general categories I. Multiplications and comultiplications" Math. Ann. , 145 (1962) pp. 227–255 |
Group object. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group_object&oldid=18656