Positive element
of an algebra 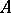 with an involution
with an involution 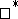
An element  of
of 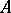 of the form
of the form 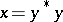 , where
, where 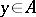 . The set
. The set 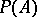 of positive elements in a Banach
of positive elements in a Banach  -algebra
-algebra 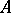 contains the set
contains the set 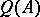 of squares of the Hermitian elements, which in turn contains the set
of squares of the Hermitian elements, which in turn contains the set 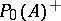 of all Hermitian elements with positive spectrum (cf. Spectrum of an element), but in general it does not contain the set
of all Hermitian elements with positive spectrum (cf. Spectrum of an element), but in general it does not contain the set 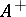 of all Hermitian elements with non-negative spectrum. The condition
of all Hermitian elements with non-negative spectrum. The condition 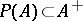 defines the class of completely-symmetric (or Hermitian) Banach
defines the class of completely-symmetric (or Hermitian) Banach  -algebras. For a
-algebras. For a  -algebra to be completely symmetric it is necessary and sufficient that all Hermitian elements in it have real spectrum. The equality
-algebra to be completely symmetric it is necessary and sufficient that all Hermitian elements in it have real spectrum. The equality 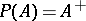 holds if and only if
holds if and only if 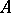 is a
is a 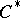 -algebra. In that case
-algebra. In that case 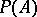 is a reproducing cone (cf. Semi-ordered space) in the space of all Hermitian elements of the algebra
is a reproducing cone (cf. Semi-ordered space) in the space of all Hermitian elements of the algebra 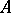 .
.
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [2] | J. Dixmier, "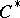 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [3] | D.N. Raikov, Dokl. Akad. Nauk. SSSR , 54 : 5 (1946) pp. 391–394 |
| [4] | V. Pták, "On the spectral radius in Banach algebras with involution" Bull. London Math. Soc. , 2 (1970) pp. 327–334 |
| [5] | T.W. Palmer, "Hermitian Banach  -algebras" Bull. Amer. Math. Soc. , 78 (1972) pp. 522–524 -algebras" Bull. Amer. Math. Soc. , 78 (1972) pp. 522–524 |
Positive element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_element&oldid=18639