Projective spectrum of a ring
A scheme  associated with a graded ring
associated with a graded ring  (cf. also Graded module). As a set of points,
(cf. also Graded module). As a set of points,  is a set of homogeneous prime ideals
is a set of homogeneous prime ideals  such that
such that  does not contain
does not contain  . The topology on
. The topology on  is defined by the following basis of open sets:
is defined by the following basis of open sets:  for
for  ,
,  . The structure sheaf
. The structure sheaf 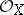 of the locally ringed space
of the locally ringed space  is defined on the basis open sets as follows:
is defined on the basis open sets as follows: 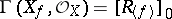 , that is, the subring of the elements of degree
, that is, the subring of the elements of degree  of the ring
of the ring  of fractions with respect to the multiplicative system
of fractions with respect to the multiplicative system 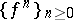 .
.
The most important example of a projective spectrum is  . The set of its
. The set of its 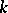 -valued points
-valued points  for any field
for any field 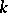 is in natural correspondence with the set of points of the
is in natural correspondence with the set of points of the  -dimensional projective space over the field
-dimensional projective space over the field 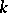 .
.
If all the rings 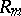 as
as  -modules are spanned by
-modules are spanned by 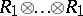 (
( terms), then an additional structure is defined on
terms), then an additional structure is defined on 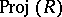 . Namely, the covering
. Namely, the covering 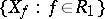 and the units
and the units 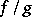 determine a Čech
determine a Čech 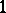 -cocycle on
-cocycle on 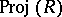 to which an invertible sheaf, denoted by
to which an invertible sheaf, denoted by  , corresponds. The symbol
, corresponds. The symbol 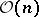 usually denotes the
usually denotes the  -th tensor power
-th tensor power 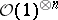 of
of  . There exists a canonical homomorphism
. There exists a canonical homomorphism 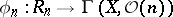 , indicating the geometric meaning of the grading of the ring
, indicating the geometric meaning of the grading of the ring  (see [1]). If, for example,
(see [1]). If, for example, 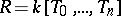 , then
, then 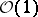 corresponds to a sheaf of hyperplane sections in
corresponds to a sheaf of hyperplane sections in 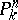 .
.
References
| [1] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) |
| [2] | A. Grothendieck, "Eléments de géometrie algebrique" Publ. Math. IHES , 1–4 (1960–1967) |
Comments
See also Projective scheme.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 91 |
Projective spectrum of a ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_spectrum_of_a_ring&oldid=18513