Section of a mapping
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A mapping 
for which 
. In a wider sense, a section of any morphism in an arbitrary category is a right-inverse morphism.
Comments
If 
is a subspace of 
, a section over 
of 
is a mapping 
such that 
for all 
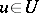. For a vector bundle 
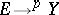, where the mapping 
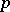is part of the structure defined, one speaks of a section of the vector bundle 
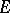rather than of a section of 
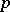. This applies, e.g., also to sheaves and fibrations. A standard notation for the set of sections in such a case is 
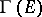, or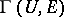 
for the set of sections of 
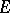over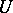 
.
How to Cite This Entry:
Section of a mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Section_of_a_mapping&oldid=18495
Section of a mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Section_of_a_mapping&oldid=18495
This article was adapted from an original article by A.F. Kharshiladze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article