Titchmarsh problem

The problem of finding an asymptotic expression for

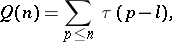(1)

where 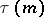is the number of divisors of 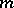(cf. Divisor problems), 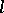is a fixed non-zero number and 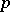runs through all prime numbers. Analogous to this problem is the problem of finding an asymptotic expression for

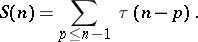(2)

This problem was posed by E. Titchmarsh (1930) and was solved by him [1] under the assumption that the Riemann hypothesis is true (cf. Riemann hypotheses).

The dispersion method, developed by Yu.V. Linnik, allows one to find asymptotics for (1) and (2):

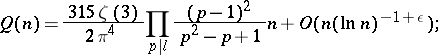the formula for 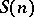is analogous.

The Vinogradov–Bombieri theorem on the average distribution of prime numbers in arithmetic progressions also leads to a solution of the Titchmarsh problem. Here the assumption of the truth of the Riemann hypothesis is actually replaced by theorems of the large sieve type.

References

[1]	Yu.V. Linnik, "The dispersion method in binary additive problems" , Amer. Math. Soc. (1963) (Translated from Russian)
[2]	B.M. Bredikhin, "The dispersion method and binary additive problems" Russian Math. Surveys , 20 : 2 (1965) pp. 85–125 Uspekhi Mat. Nauk , 20 : 2 (1965) pp. 89–130
[3]	K. Prachar, "Primzahlverteilung" , Springer (1957)