Schwarz equation
The non-linear ordinary differential equation of the third order
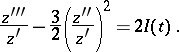 | (1) |
Its left-hand side is called the Schwarzian derivative of the function 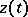 and is denoted by
and is denoted by 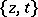 . H.A. Schwarz applied this equation in his studies [1].
. H.A. Schwarz applied this equation in his studies [1].
If  is a fundamental system of solutions of the second-order linear differential equation
is a fundamental system of solutions of the second-order linear differential equation
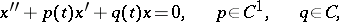 | (2) |
then on any interval where  , the function
, the function
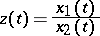 | (3) |
satisfies the Schwarz equation (1), where
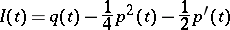 |
is the so-called invariant of the linear equation (2). Conversely, any solution of the Schwarz equation (1) can be presented in the form (3), where 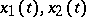 are linearly independent solutions of (2). Solutions of a Schwarz equation with a rational right-hand side in the complex plane are closely connected with the problem of describing the functions that conformally map the upper half-plane into a polygon bounded by a finite number of segments of straight lines and arcs of circles.
are linearly independent solutions of (2). Solutions of a Schwarz equation with a rational right-hand side in the complex plane are closely connected with the problem of describing the functions that conformally map the upper half-plane into a polygon bounded by a finite number of segments of straight lines and arcs of circles.
References
| [1] | H.A. Schwarz, "Ueber diejenigen Fälle, in welchen die Gaussische hypergeometrische Reihe eine algebraische Function ihres vierten Elements darstellt (nebst zwei Figurtafeln)" J. Reine Angew. Math. , 75 (1873) pp. 292–335 |
| [2] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
Comments
For the relation with conformal mapping see [a2] and Christoffel–Schwarz formula.
References
| [a1] | E. Hille, "Lectures on ordinary differential equations" , Addison-Wesley (1969) |
| [a2] | Z. Nehari, "Conformal mapping" , Dover, reprint (1975) pp. Chapt. 7, §7 |
Schwarz equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schwarz_equation&oldid=18412