Nash theorem (in game theory)
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A theorem on the existence of equilibrium points in a mixed extension of a finite non-cooperative game
 |
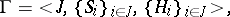where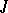 
and 
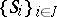are the finite sets of players and their strategies, respectively, and 
: 
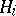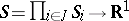is the pay-off function of player 
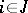(see also Games, theory of). It was established by J. Nash in [1]. Let 
, 
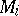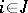, be the set of all probability measures on 
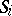. Nash' theorem asserts that there is a measure 
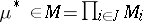for which
 |
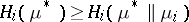for all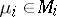 
, 
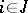, where 
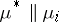denotes the measure from 
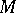that results from replacing the 
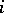-th component of the vector 
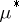by 
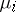, and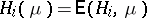 
. The known proofs of Nash' theorem rely on a fixed-point theorem.
References
| [1] | J. Nash, "Non-cooperative games" Ann. of Math. , 54 (1951) pp. 286–295 |
| [2] | N.N. Vorob'ev, "Foundations of game theory. Non-cooperative games" , Moscow (1984) (In Russian) |
| [3] | N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian) |
How to Cite This Entry:
Nash theorem (in game theory). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nash_theorem_(in_game_theory)&oldid=18406
Nash theorem (in game theory). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nash_theorem_(in_game_theory)&oldid=18406
This article was adapted from an original article by E.B. Yanovskaya (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article