Number of divisors
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A function of a natural argument, 
, equal to the number of natural divisors of the number 
. This arithmetic function is denoted by 
or 
. The following formula holds:
 |
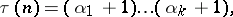where
 |
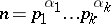is the canonical expansion of 
into prime factors. For prime numbers 
, 
, but there exists an infinite sequence of 
for which
 |
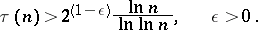On the other hand, for all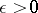 
,
 |
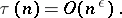is a multiplicative arithmetic function and is equal to the number of points with natural coordinates on the hyperbola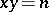 
. The average value of 
is given by Dirichlet's asymptotic formula (cf. Divisor problems). The function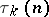 
, which is the number of solutions of the equation 
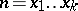in natural numbers 
, is a generalization of the function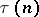 
.
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
| [2] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XVI |
How to Cite This Entry:
Number of divisors. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Number_of_divisors&oldid=18293
Number of divisors. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Number_of_divisors&oldid=18293
This article was adapted from an original article by N.I. Klimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article