Extension of a differential field
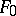
A differential field 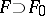 with a set
with a set 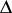 of differentiations such that the set of restrictions of the elements of
of differentiations such that the set of restrictions of the elements of 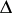 to
to 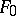 coincides with the set of differentiations on
coincides with the set of differentiations on 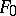 . In turn,
. In turn, 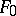 is a differential subfield of
is a differential subfield of 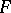 .
.
The intersection of any set of differential subfields of 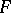 is again a differential subfield of
is again a differential subfield of 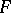 . For any set of elements
. For any set of elements 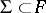 there is a smallest differential subfield of
there is a smallest differential subfield of 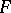 containing all the elements of
containing all the elements of 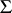 and
and 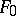 ; it is denoted by
; it is denoted by 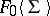 and is called the extension of the field
and is called the extension of the field 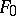 generated by the set
generated by the set 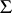 (and
(and 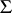 is called a set, or family, of generators of the extension
is called a set, or family, of generators of the extension 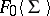 over
over 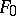 ). The extension is said to be finitely generated if it has a finite set of generators, and is called simply generated if the set of generators consists of one element. If
). The extension is said to be finitely generated if it has a finite set of generators, and is called simply generated if the set of generators consists of one element. If 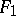 and
and 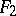 are two differential subfields of
are two differential subfields of 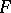 , then the subfield
, then the subfield
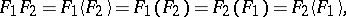 |
is a differential subfield of 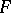 , called the join of the fields
, called the join of the fields 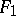 and
and 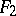 .
.
Let 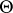 be the free commutative semi-group generated by
be the free commutative semi-group generated by 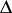 (its elements are called differential operators). A family
(its elements are called differential operators). A family 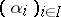 of elements of
of elements of 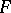 is said to be differentially algebraically dependent over
is said to be differentially algebraically dependent over 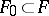 if the family
if the family 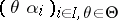 is algebraically dependent over
is algebraically dependent over 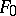 . In the opposite case, the family
. In the opposite case, the family  is called differentially algebraically independent over
is called differentially algebraically independent over 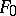 , or a family of differential indeterminates over
, or a family of differential indeterminates over 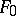 . One says that the elements of
. One says that the elements of 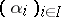 are differentially separably dependent over
are differentially separably dependent over 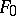 if the family
if the family 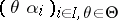 is separably dependent over
is separably dependent over 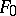 . In the opposite case the family
. In the opposite case the family 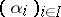 is called differentially separably independent over
is called differentially separably independent over 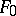 .
.
An extension 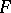 is called differentially algebraic over
is called differentially algebraic over 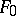 if every element of
if every element of 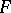 is differentially algebraic over
is differentially algebraic over 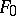 . Similarly,
. Similarly, 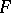 is called differentially separable over
is called differentially separable over 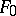 if every element of
if every element of 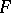 is differentially separable over
is differentially separable over 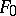 . The theorem on the primitive element applies to differential extensions: If the set
. The theorem on the primitive element applies to differential extensions: If the set  is independent over
is independent over 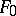 , then every finitely-generated differentially-separable extension
, then every finitely-generated differentially-separable extension 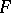 of
of 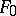 is generated by one element.
is generated by one element.
Let 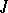 be a given set and let
be a given set and let 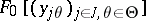 be the polynomial algebra over
be the polynomial algebra over 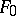 in the family of indeterminates
in the family of indeterminates 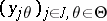 , with index set
, with index set 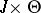 . Any differentiation
. Any differentiation 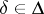 of
of 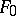 extends in a unique way to a differentiation of
extends in a unique way to a differentiation of 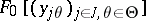 sending
sending 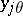 to
to 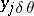 . This differential ring is called the ring of differential polynomials in the differential indeterminates
. This differential ring is called the ring of differential polynomials in the differential indeterminates 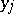 ,
, 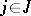 , and is denoted by
, and is denoted by 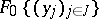 . Its differential field of fractions (i.e. the field of fractions with extended differentiations) is denoted by
. Its differential field of fractions (i.e. the field of fractions with extended differentiations) is denoted by 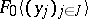 , and the elements of this field are called differential functions over
, and the elements of this field are called differential functions over 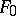 in the differential indeterminates
in the differential indeterminates 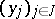 . For ordinary differential fields an analogue of the Lüroth theorem holds: If
. For ordinary differential fields an analogue of the Lüroth theorem holds: If 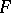 is an arbitrary differential extension of a differential field
is an arbitrary differential extension of a differential field 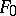 contained in
contained in 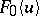 , then
, then 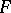 contains an element
contains an element  such that
such that 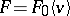 .
.
For any differential field 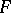 there is a separable semi-universal extension, i.e. an extension containing every finitely-generated separable extension of
there is a separable semi-universal extension, i.e. an extension containing every finitely-generated separable extension of 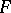 . Moreover, there exists a separable universal extension
. Moreover, there exists a separable universal extension 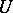 , i.e. an extension which is semi-universal over every finitely-generated extension of
, i.e. an extension which is semi-universal over every finitely-generated extension of 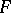 contained in
contained in 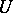 .
.
In the theory of differential fields there is no direct analogue of the notion of an algebraically closed field in ordinary field theory. To a certain extent, their role is played by constrainedly closed fields. The main property of such a field 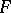 is that any finite system of algebraic differential equations and inequalities with coefficients in
is that any finite system of algebraic differential equations and inequalities with coefficients in 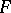 having a solution that is rational over some field extension of
having a solution that is rational over some field extension of 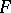 has a solution that is rational over
has a solution that is rational over 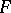 . A family
. A family 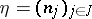 of elements of some extension of
of elements of some extension of 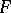 is called constrained over
is called constrained over 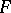 if there is a differential polynomial
if there is a differential polynomial 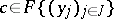 such that
such that  and
and  for any non-generic differential specialization
for any non-generic differential specialization 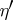 of the point
of the point 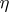 over
over 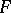 . An extension
. An extension 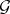 of
of 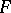 is called constrained over
is called constrained over 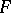 if any finite set of elements
if any finite set of elements 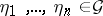 is constrained over
is constrained over 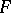 . This is equivalent to saying that an arbitrary element of
. This is equivalent to saying that an arbitrary element of 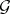 is constrained over
is constrained over 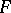 . A differential field having no non-trivial constrained extensions is called constrainedly closed. An example of such a field is the universal differential field of characteristic zero (the universal field extension of the field of rational numbers
. A differential field having no non-trivial constrained extensions is called constrainedly closed. An example of such a field is the universal differential field of characteristic zero (the universal field extension of the field of rational numbers 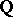 ). Any differential field
). Any differential field 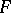 of characteristic zero has a constrained closure, i.e. a constrainedly closed extension of
of characteristic zero has a constrained closure, i.e. a constrainedly closed extension of 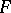 which is contained in any other constrainedly closed extension of
which is contained in any other constrainedly closed extension of 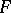 .
.
The notion of a normal extension in ordinary field theory carries over to differential algebra in various ways. In differential Galois theory, a fundamental role is played by strongly normal extensions. Let 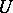 be the fixed universal differential field of characteristic 0 with field of constants
be the fixed universal differential field of characteristic 0 with field of constants 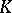 . All the differential fields encountered below are assumed to lie in
. All the differential fields encountered below are assumed to lie in 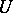 and all isomorphisms are assumed to be differential isomorphisms, that is, they commute with the operators in
and all isomorphisms are assumed to be differential isomorphisms, that is, they commute with the operators in 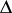 . Let
. Let 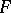 and
and 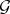 be differential fields over which
be differential fields over which 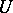 is universal. Let
is universal. Let  be the field of constants of
be the field of constants of 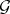 . An isomorphism
. An isomorphism 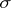 leaves invariant each element of
leaves invariant each element of 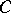 ,
, 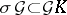 , and
, and 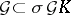 (that is,
(that is, 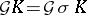 ). A strongly normal extension of
). A strongly normal extension of 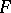 is a finitely-generated extension
is a finitely-generated extension 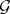 of
of 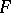 such that every isomorphism of
such that every isomorphism of  over
over 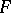 is strong. Strongly normal extensions are constrained. The set of strong isomorphisms of a strongly normal extension
is strong. Strongly normal extensions are constrained. The set of strong isomorphisms of a strongly normal extension 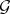 over
over  has the natural structure of an algebraic group, defined over
has the natural structure of an algebraic group, defined over 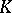 (and denoted by
(and denoted by  ). This is the Galois differential group of the extension
). This is the Galois differential group of the extension  . A special case of strongly normal extensions is given by the Picard–Vessiot extensions, i.e. extensions that preserve the field of constants and result from the adjunction to
. A special case of strongly normal extensions is given by the Picard–Vessiot extensions, i.e. extensions that preserve the field of constants and result from the adjunction to 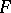 of a basis for the solutions of some system of homogeneous linear differential equations with coefficients in
of a basis for the solutions of some system of homogeneous linear differential equations with coefficients in 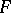 . For extensions of this type,
. For extensions of this type, 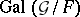 is an algebraic matrix group, i.e. an algebraic subgroup of the group
is an algebraic matrix group, i.e. an algebraic subgroup of the group 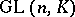 for some integer
for some integer 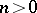 .
.
The Galois differential groups of some typical differential algebraic extensions have the following form.
1) Let  , where
, where 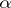 satisfies the system of equations
satisfies the system of equations  ,
,  ,
, 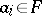 ,
,  , and let the fields of constants of
, and let the fields of constants of 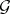 and
and  coincide. Then
coincide. Then 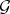 is a Picard–Vessiot extension of
is a Picard–Vessiot extension of 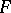 and the Galois differential group
and the Galois differential group 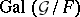 is a subgroup of the multiplicative group of
is a subgroup of the multiplicative group of 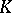 (that is,
(that is, 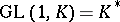 ). If
). If 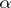 is algebraic, it satisfies an equation of the form
is algebraic, it satisfies an equation of the form 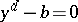 , where
, where 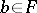 and
and 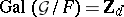 (the group of
(the group of 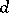 -th roots of unity). In this case,
-th roots of unity). In this case, 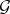 is called an extension of
is called an extension of 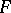 by an exponent.
by an exponent.
2) Let 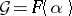 , where
, where  satisfies the system of equations
satisfies the system of equations  ,
, 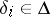 ,
, 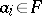 ,
, 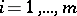 (such an element
(such an element  is called primitive over
is called primitive over 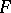 ), and let the field of constants of
), and let the field of constants of 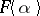 coincide with
coincide with 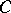 . If
. If 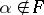 , then
, then 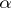 is transcendental over
is transcendental over 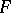 . The resulting extension is a Picard–Vessiot extension, and the Galois group
. The resulting extension is a Picard–Vessiot extension, and the Galois group  is isomorphic to the additive group of
is isomorphic to the additive group of 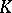 . Such extensions are called extensions by an integral.
. Such extensions are called extensions by an integral.
3) Let 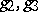 be elements of
be elements of 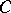 such that
such that 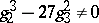 . An element
. An element 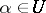 is said to be Weierstrass over
is said to be Weierstrass over 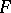 if
if 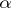 satisfies the system of equations
satisfies the system of equations 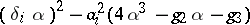 ,
, 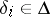 ,
, 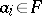 ,
,  . The extension
. The extension 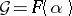 is strongly normal over
is strongly normal over 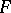 , but if
, but if 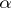 is transcendental over
is transcendental over 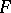 , it is not a Picard–Vessiot extension. There is a monomorphism
, it is not a Picard–Vessiot extension. There is a monomorphism
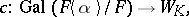 |
where 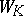 is the group of points on the cubic curve
is the group of points on the cubic curve
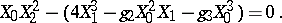 |
If 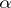 is transcendental over
is transcendental over 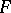 , then
, then  is an isomorphism.
is an isomorphism.
4) Let 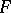 be a differential field,
be a differential field, 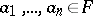 , and let
, and let 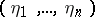 be the fundamental set of zeros of the equation
be the fundamental set of zeros of the equation 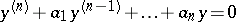 , which generates the Picard–Vessiot extension of
, which generates the Picard–Vessiot extension of 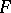 . The Galois group
. The Galois group 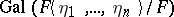 is contained in
is contained in 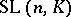 if and only if the equation
if and only if the equation  has a non-trivial zero in
has a non-trivial zero in 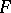 . In particular, if
. In particular, if 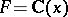 is the differential field of rational functions of one complex variable with differentiation
is the differential field of rational functions of one complex variable with differentiation 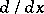 and
and 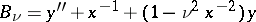 is the Bessel differential polynomial, then the Galois group of the corresponding extension coincides with
is the Bessel differential polynomial, then the Galois group of the corresponding extension coincides with 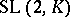 for
for 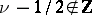 . If
. If  , then the Galois group coincides with
, then the Galois group coincides with 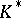 .
.
For all positive integers  one can construct extensions of differential fields
one can construct extensions of differential fields 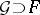 such that
such that 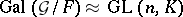 .
.
A Galois correspondence exists between the set of differential subfields of a strongly normal extension and the set of algebraic subgroups of its Galois group.
As in ordinary Galois theory, two general problems are of interest in the differential case.
a) The direct problem: Given a strongly normal extension 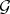 of a differential field
of a differential field 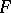 , determine its Galois group.
, determine its Galois group.
b) The converse problem: Given a differential field 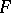 and an algebraic group
and an algebraic group 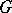 , describe the set of strongly normal extensions of
, describe the set of strongly normal extensions of 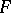 with Galois group isomorphic to
with Galois group isomorphic to 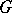 (in particular, determine if it is non-empty).
(in particular, determine if it is non-empty).
There is another way of generalizing normality in the case of extensions of differential fields and of constructing a differential Galois theory; this uses methods of differential geometry [4].
References
| [1] | J.F. Ritt, "Differential algebra" , Amer. Math. Soc. (1950) |
| [2] | E.R. Kolchin, "Differential algebra and algebraic groups" , Acad. Press (1973) |
| [3] | I. Kaplansky, "An introduction to differential algebra" , Hermann (1976) |
| [4] | J.F. Pommaret, "Differential Galois theory" , Gordon & Breach (1983) |
Extension of a differential field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extension_of_a_differential_field&oldid=18279