Torsion submodule
Let 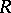 be an associative ring with unit, and
be an associative ring with unit, and 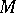 a left
a left 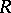 -module. The torsion subgroup
-module. The torsion subgroup 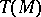 is defined as
is defined as
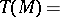 |
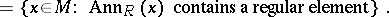 |
Here a regular element 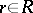 is an element that is not a zero divisor (neither left nor right).
is an element that is not a zero divisor (neither left nor right).
If 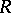 is left Ore (cf. below and Associative rings and algebras), then
is left Ore (cf. below and Associative rings and algebras), then 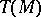 is a submodule of
is a submodule of 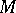 , called the torsion submodule. A module
, called the torsion submodule. A module 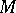 is torsion free if
is torsion free if 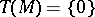 . A module is torsion if
. A module is torsion if 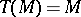 .
.
Quite generally, a torsion theory for an Abelian category 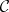 is a pair
is a pair 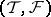 of subclasses of the objects of
of subclasses of the objects of 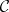 such that
such that 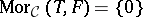 for all
for all 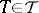 ,
, 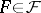 and
and 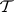 and
and 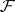 are maximal with this property, i.e. if
are maximal with this property, i.e. if  for all
for all  , then
, then  , and if
, and if 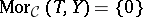 for all
for all 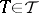 , then
, then 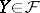 .
.
The torsion submodules and torsion-free submodules of a left Ore ring 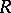 from a torsion theory for the category
from a torsion theory for the category 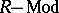 of left
of left 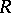 -modules.
-modules.
A radical on 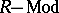 is a left-exact functor
is a left-exact functor 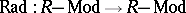 such that for all
such that for all 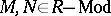 ,
,
i) 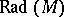 is a submodule of
is a submodule of 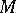 ;
;
ii) 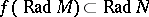 for all
for all 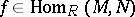 ; more precisely,
; more precisely, 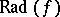 is the restriction of
is the restriction of 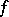 to
to 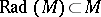 .
.
iii) 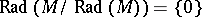 .
.
A radical 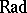 is a torsion radical or hereditary radical if
is a torsion radical or hereditary radical if 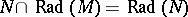 for each submodule
for each submodule 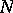 of a module
of a module 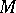 . A torsion radical
. A torsion radical 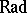 defines a torsion theory for
defines a torsion theory for 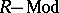 with
with 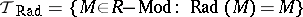 ,
, 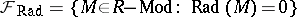 . All torsion theories for
. All torsion theories for 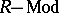 arise this way.
arise this way.
A left denominator set of 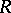 is a submonoid
is a submonoid 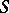 of
of 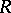 (i.e.
(i.e. 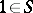 and
and 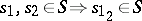 ) such that:
) such that:
a) (the left Ore condition) for all 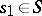 ,
, 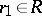 there are
there are 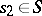 ,
,  such that
such that  ;
;
b) if 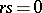 for
for 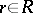 ,
, 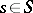 , then there is an
, then there is an 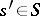 with
with 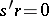 .
.
If the set of all regular elements of 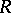 is a left denominator set, then
is a left denominator set, then 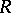 is called left Ore. A left denominator set is also called a left Ore set.
is called left Ore. A left denominator set is also called a left Ore set.
A left denominator set 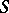 defines a torsion theory
defines a torsion theory 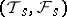 for
for 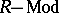 by the associated radical functor
by the associated radical functor
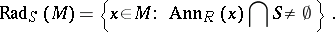 |
This illustrates the links between torsion theories and (non-commutative) localization (theories). For much more about this theme cf. [a1], [a2], [a3], cf. also Fractions, ring of.
References
| [a1] | L.H. Rowen, "Ring theory" , 1 , Acad. Press (1988) pp. §3.4 |
| [a2] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) pp. §15, §16 |
| [a3] | J.S. Golan, "Localization of noncommutative rings" , M. Dekker (1975) |
Torsion submodule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torsion_submodule&oldid=18242