Hellinger integral
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
An integral of Riemann type of a set function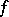 
. If 
is a space with a finite, non-negative, non-singular measure; if 
, 
, is a totally-additive function with 
for 
; and if 
is a partition of 
, then
 |
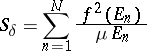and the Hellinger integral of 
with respect to 
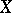is defined as
 |
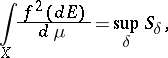provided that this supremum is finite. Hellinger's integral can also be regarded as the limit over a directed set of partitions: 
if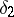 
is a subdivision of 
.
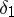If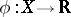 
is a summable function such that 
is the Lebesgue integral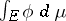 
, then the Hellinger integral can be expressed in terms of the Lebesgue integral:
 |
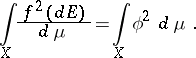E. Hellinger in [1] defined the integral for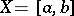 
in terms of point functions.
References
| [1] | E. Hellinger, "Neue Begründung der Theorie quadratischer Formen von unendlichvielen Veränderlichen" J. Reine Angew. Math. , 136 (1909) pp. 210–271 |
| [2] | V.I. Smirnov, "A course of higher mathematics" , 5 , Addison-Wesley (1964) (Translated from Russian) |
How to Cite This Entry:
Hellinger integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hellinger_integral&oldid=18237
Hellinger integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hellinger_integral&oldid=18237
This article was adapted from an original article by I.A. Vinogradova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article