Dirac spinor

A four-component complex function in the four-dimensional space-time which satisfies the Dirac equation. In spinor analysis, the Dirac spinor is defined as a bi-spinor of the first rank, realizing the irreducible linear representation of the general Lorentz group on 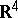with the pseudo-Euclidean metric

The Dirac matrices, which form part of the Dirac equation, are defined up to an arbitrary unitary transformation, so that the Dirac spinor is also defined up to such a unitary transformation. This property makes it possible to select the physically most convenient representation of the Dirac matrices and, consequently, of the Dirac spinor.

Comments

For references see – of Dirac equation.