Cocycle
A cochain which is annihilated by the coboundary mapping, in other words, a cochain that vanishes on boundary chains. The concept of a cocycle generalizes the concept of a closed differential form on a smooth manifold with a vanishing integral over a boundary chain.
In accordance with the different versions of the concept of a cochain, there are different versions of cocycles. For example, an Aleksandrov–Čech cocycle in a topological space is a cocycle of the nerve of some open covering of the space. Only one-dimensional cocycles with non-Abelian coefficients need special discussion. A one-dimensional cocycle of a simplicial set  with coefficients in a non-Abelian group
with coefficients in a non-Abelian group 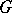 is a function
is a function 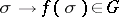 , defined on the set
, defined on the set 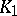 of one-dimensional simplices of
of one-dimensional simplices of 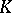 , such that
, such that 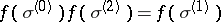 for any two-dimensional simplex
for any two-dimensional simplex  . Two cocycles
. Two cocycles 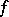 and
and  are said to be cohomologous if there exists a function
are said to be cohomologous if there exists a function 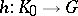 such that
such that 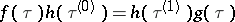 for any one-dimensional simplex
for any one-dimensional simplex 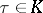 . The cohomology classes of one-dimensional cocycles form a pointed set
. The cohomology classes of one-dimensional cocycles form a pointed set 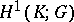 . Similarly one defines one-dimensional cocycles and their cohomology classes in the Aleksandrov–Čech sense, with coefficients in a sheaf of non-Abelian groups. The cohomology groups of these cocycles are related to fibre bundles with a structure group.
. Similarly one defines one-dimensional cocycles and their cohomology classes in the Aleksandrov–Čech sense, with coefficients in a sheaf of non-Abelian groups. The cohomology groups of these cocycles are related to fibre bundles with a structure group.
For references see Cochain.
Cocycle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cocycle&oldid=18113