Special linear group

of degree (order) over a ring

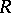
The subgroup 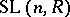of the general linear group 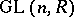which is the kernel of a determinant homomorphism 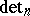. The structure of 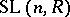depends on 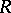, and the type of determinant defined on 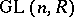. There are three main types of determinants of importance here: the ordinary determinant in the case when 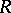is a commutative ring, the non-commutative Dieudonné determinant (cf. Determinant) when 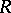is a division ring (see [1]), and the reduced norm homomorphism for a division ring that is finite dimensional over its centre (see [2]).

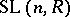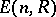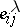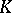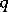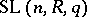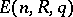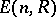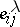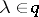has the following noteworthy subgroups: the group generated by the elementary matrices (see Algebraic -theory) and, for every two-sided ideal of , the congruence subgroup and the group which is the normal subgroup of generated by the matrices for . Let 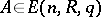and let

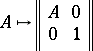be the imbedding of 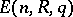into 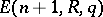. Then passage to the direct limit gives the group 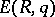. The group 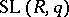is defined in a similar way. When 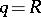one writes 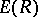and 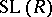instead of 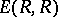and 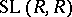, respectively. The latter is called the stable special linear group of the ring 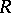. The normal subgroup structure of 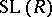is closely connected with the structure of the groups 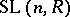: A subgroup 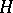is normal in 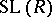if and only if, for some (unique) two-sided ideal 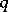of 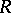, the following inclusions hold:

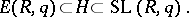Thus, the Abelian groups 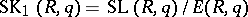classify the normal subgroups of . The group 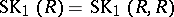is called the reduced Whitehead group of 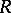. A satisfactory description of the normal subgroup structure of 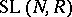for an arbitrary ring 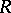uses a condition involving the stable rank of the ideal 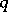(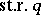). Namely, if , then there is an isomorphism

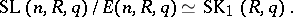In addition, if the conditions 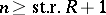, 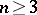hold, then for every normal subgroup 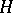of 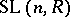the inclusions

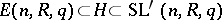hold for an appropriate 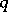, where 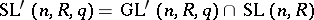, and 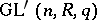is the pre-image of the centre of 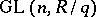in 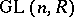. For certain special rings definitive results are known (see [2], [4], for example).

In the case of the non-commutative Dieudonné determinant (so that 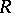is a division ring), the results are exhaustive. The groups 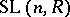and 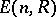coincide. 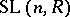is the commutator subgroup of 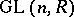, except in the case of 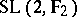(where 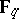denotes the field of 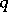elements). The centre 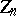of 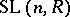consists of the scalar matrices 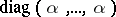, where 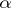is an element of the centre of 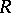and 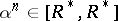, 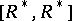being the commutator subgroup of the multiplicative group 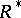of the division ring 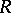. The quotient group 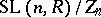is simple except when 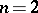and 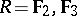. When 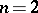, 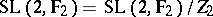and 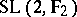is isomorphic to the symmetric group 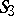of degree 3, while 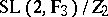is isomorphic to the alternating group 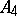of degree 4.

If is a reduced norm homomorphism, then

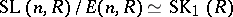and

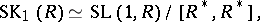so that the group 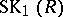is trivial when 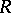is a field. The conjecture that 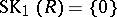for any division ring 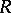stood for a long time. However, in 1975 it was shown that this is not true (see [5]). The groups 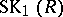play an important role in algebraic geometry (see [6], [7]). There are also generalizations of the reduced norm homomorphism, which have stimulated a series of new investigations into special linear groups.

References

[1]	E. Artin, "Geometric algebra" , Interscience (1957)
[2]	H. Bass, "Algebraic -theory" , Benjamin (1968)
[3]	J.W. Milnor, "Introduction to algebraic -theory" , Princeton Univ. Press (1971)
[4]	A.A. Suslin, "On the structure of the special linear group over polynomial rings" Math. USSR Izv. , 11 (1977) pp. 211–238 Izv. Akad. Nauk SSSR Ser. Mat. , 41 : 2 (1977) pp. 235–252
[5]	V.P. Platonov, "A problem of Tannaka–Artin and groups of projective conorms" Soviet Math. Dokl. , 16 (1975) pp. 781–786 Dokl. Akad. Nauk SSSR , 222 : 2 (1975) pp. 1299–1302
[6]	V.P. Platonov, "The Tannaka–Artin problem and reduced -theory" Math. USSR Izv. , 10 (1976) pp. 211–243 Izv. Akad. Nauk SSSR Ser. Mat. , 40 : 2 (1976) pp. 227–261
[7]	V.P. Platonov, "Algebraic groups and reduced 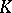-theory" , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , 1 , Acad. Sci. Fennicae (1980) pp. 311–323

Comments

For the reduced norm homomorphism see Reduced norm.

References

[a1]	A.J. Hahn, O.T. O'Meara, "The classical groups and 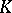-theory" , Springer (1989)