Hilbert kernel
From Encyclopedia of Mathematics
The kernel of the Hilbert singular integral, i.e. the function
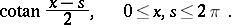 |
The following simple relation holds between the Hilbert kernel and the Cauchy kernel in the case of the unit circle:
 |
where 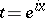 ,
, 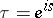 .
.
Comments
References
| [a1] | B.L. Moiseiwitsch, "Integral equations" , Longman (1977) |
How to Cite This Entry:
Hilbert kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_kernel&oldid=18062
Hilbert kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_kernel&oldid=18062
This article was adapted from an original article by B.V. Khvedelidze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article