Positive-definite operator
From Encyclopedia of Mathematics
A symmetric operator 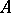 on a Hilbert space
on a Hilbert space 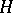 such that
such that
 |
for any 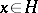 ,
, 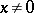 . Any positive-definite operator is a positive operator.
. Any positive-definite operator is a positive operator.
Comments
More generally, a positive-definite operator is defined as a bounded symmetric (i.e. self-adjoint) operator such that 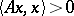 for all
for all  . This includes the diagonal operator, which acts on a basis
. This includes the diagonal operator, which acts on a basis 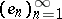 of a Hilbert space as
of a Hilbert space as 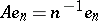 . A non-negative-definite operator is one for which
. A non-negative-definite operator is one for which 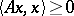 for all
for all 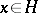 , cf. [a2]. Sometimes a non-negative-definite operator is called a positive operator.
, cf. [a2]. Sometimes a non-negative-definite operator is called a positive operator.
References
| [a1] | E. Hille, "Methods in classical and functional analysis" , Addison-Wesley (1972) |
| [a2] | N. Dunford, J.T. Schwartz, "Linear operators" , 1–3 , Interscience (1958–1971) pp. 906 |
How to Cite This Entry:
Positive-definite operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive-definite_operator&oldid=18058
Positive-definite operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive-definite_operator&oldid=18058
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article