Darboux tensor
A symmetric tensor of valency three,
 |
where 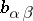 are the coefficients of the second fundamental form of the surface,
are the coefficients of the second fundamental form of the surface, 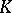 is the Gaussian curvature, and
is the Gaussian curvature, and 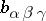 and
and 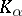 are their covariant derivatives. G. Darboux [1] was the first to investigate this tensor in special coordinates.
are their covariant derivatives. G. Darboux [1] was the first to investigate this tensor in special coordinates.
The cubic differential form
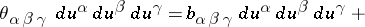 |
 |
is connected with the Darboux tensor. This form, evaluated for a curve on a surface, is known as the Darboux invariant. On a surface of constant negative curvature the Darboux invariant coincides with the differential parameter on any one of its curves. A curve at each point of which the Darboux invariant vanishes is known as a Darboux curve. Only one real family of Darboux curves exists on a non-ruled surface of negative curvature. Three real families of Darboux curves exist on a surface of positive curvature. A surface at each point of which the Darboux tensor is defined and vanishes identically is called a Darboux surface. Darboux surfaces are second-order surfaces which are not developable on a plane.
References
| [1] | G. Darboux, "Etude géométrique sur les percussions et le choc des corps" Bull. Sci. Math. Ser. 2 , 4 (1880) pp. 126–160 |
| [2] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 2 , Moscow-Leningrad (1948) pp. 210–233 (In Russian) |
Comments
References
| [a1] | G. Fubini, E. Čech, "Introduction á la géométrie projective différentielle des surfaces" , Gauthier-Villars (1931) |
| [a2] | G. Bol, "Projective Differentialgeometrie" , Vandenhoeck & Ruprecht (1954) |
| [a3] | E.P. Lane, "A treatise on projective differential geometry" , Univ. Chicago Press (1942) |
Darboux tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_tensor&oldid=18025