Hermitian kernel

A complex-valued function 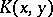that is square-integrable on and satisfies the condition (of Hermitian symmetry)

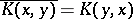(1)

for almost-all 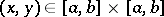. The bar in (1) denotes transition to the complex-conjugate value. If a Hermitian kernel vanishes almost nowhere, then it has at least one characteristic (eigen) value, that is, there exists a number 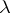such that the equation

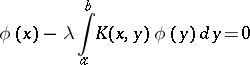has a non-zero solution (an eigen function corresponding to 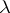). All eigen values are real and on any interval there are only finitely many. The eigen functions corresponding to distinct eigen values are orthogonal to each other.

There is an orthonormal (finite or infinite) sequence of eigen functions 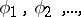corresponding to the eigen values 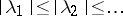. The series

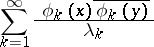(2)

converges in the mean on the square 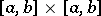to the kernel 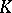. If the kernel is continuous and the series (2) converges uniformly on 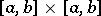, then its sum is . The system of eigen values and eigen functions of a Hermitian kernel is finite if and only if the kernel is degenerate (cf. Degenerate kernel).

All iterated kernels (cf. Iterated kernel) of a Hermitian kernel are also Hermitian.

The linear integral operator generated by a Hermitian kernel is self-adjoint. A Hermitian kernel is called complete (or closed) if the system of its eigen functions is complete in ; otherwise it is called incomplete. A Hermitian kernel is called positive (negative) if all its eigen values are positive (negative). A complete positive (negative) kernel is called positive (negative) definite.

The interval 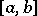can be replaced by a domain in an -dimensional Euclidean space.

References

[1]	V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) pp. Chapt. 1 (Translated from Russian)
[2]	V.S. Vladimirov, "Gleichungen der mathematischen Physik" , MIR (1984) (Translated from Russian)

Comments

Another result connected with the series (2) is Mercer's theorem: Let the kernel be continuous on 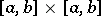and suppose that for all 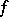in ,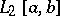

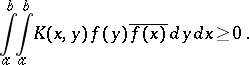If 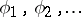is an orthonormal sequence of (continuous) eigen functions corresponding to the eigen values 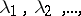then the series (2) converges absolutely and uniformly on 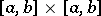and the sum of (2) is .

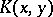References

[a1]	I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981)
[a2]	F.G. Tricomi, "Integral equations" , Interscience (1957)