Yoke
The concept of a yoke, introduced in [a3], is of great importance in relation to geometric, i.e. parametrization invariant, calculations on statistical models (cf. also Differential geometry in statistical inference; Statistical manifold). A yoke on a model  induces a metric and families of connections, derivative strings and tensors on
induces a metric and families of connections, derivative strings and tensors on  in terms of which geometric properties of
in terms of which geometric properties of 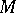 may be formulated, see [a5]. Differences and similarities between the expected and observed geometry of
may be formulated, see [a5]. Differences and similarities between the expected and observed geometry of 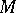 may be discussed using yokes, see [a5]. Furthermore, invariant Taylor expansions of functions defined on
may be discussed using yokes, see [a5]. Furthermore, invariant Taylor expansions of functions defined on 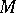 are obtainable via yokes. Finally, a relationship between yokes and symplectic forms has been established in [a4].
are obtainable via yokes. Finally, a relationship between yokes and symplectic forms has been established in [a4].
In order to define a yoke, let 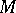 be a smooth
be a smooth  -dimensional manifold and let
-dimensional manifold and let 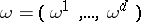 and, correspondingly,
and, correspondingly, 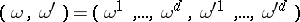 denote local coordinates on
denote local coordinates on 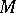 and
and 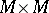 , respectively. Arbitrary components of
, respectively. Arbitrary components of 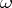 will be denoted by the letters
will be denoted by the letters 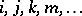 . For two sets of indices
. For two sets of indices 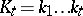 and
and 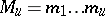 and a smooth function
and a smooth function 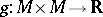 , the symbol
, the symbol 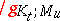 is used for the values of the function
is used for the values of the function
 |
evaluated at the diagonal of 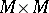 , i.e.
, i.e.
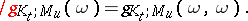 |
With this notation, a yoke is a smooth function 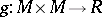 , such that for every
, such that for every 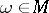 :
:
i) 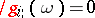 ;
;
ii) the matrix 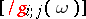 is non-singular.
is non-singular.
A normalized yoke is a yoke satisfying the additional condition 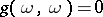 . For any yoke
. For any yoke 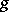 there exists a corresponding normalized yoke
there exists a corresponding normalized yoke 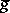 , given by
, given by 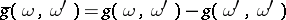 , and a dual yoke
, and a dual yoke 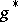 , given by
, given by 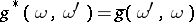 .
.
In the statistical context the two most important examples of normalized yokes are the expected and the observed likelihood yoke. For a parametric statistical model with parameter space  , sample space
, sample space 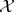 and log-likelihood function
and log-likelihood function 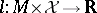 , the expected likelihood yoke is given by
, the expected likelihood yoke is given by
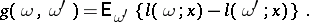 |
The observed likelihood yoke is given by
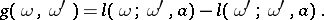 |
Here,  is an auxiliary statistic such that the function
is an auxiliary statistic such that the function 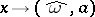 , where
, where 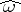 denotes the maximum-likelihood estimator of
denotes the maximum-likelihood estimator of  (cf. also Maximum-likelihood method), is bijective. Further examples of statistical yokes are related to contrast functions, see [a5].
(cf. also Maximum-likelihood method), is bijective. Further examples of statistical yokes are related to contrast functions, see [a5].
Some further notation is needed for the discussion of properties of yokes. If 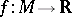 is a smooth function, one sets
is a smooth function, one sets
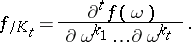 |
Furthermore, if 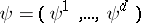 is an alternative set of local coordinates for which arbitrary components are denoted by the letters
is an alternative set of local coordinates for which arbitrary components are denoted by the letters 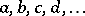 and if for
and if for 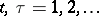
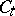 and
and 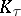 are two sets of indices related to the local coordinates
are two sets of indices related to the local coordinates 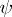 and
and 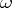 , respectively, one sets
, respectively, one sets
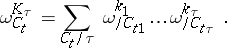 |
Here, the summation is over ordered partitions of 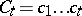 into
into  (non-empty) subsets
(non-empty) subsets 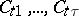 such that the order of the indices in each of the subsets is the same as the order within
such that the order of the indices in each of the subsets is the same as the order within 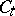 and such that for
and such that for  the first index of
the first index of 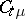 comes before the first index of
comes before the first index of 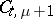 as compared with the ordering within
as compared with the ordering within 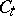 . For
. For 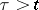 , the sum is to be interpreted as
, the sum is to be interpreted as  .
.
Let 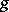 be an arbitrary yoke and let
be an arbitrary yoke and let 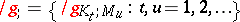 . Then the most important properties of
. Then the most important properties of 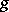 are:
are:
a)  satisfies the balance relation
satisfies the balance relation
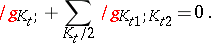 |
b) 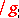 is a double derivative string, i.e. the transformation law is
is a double derivative string, i.e. the transformation law is
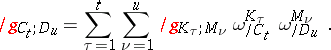 |
In particular, 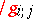 is a symmetric non-singular
is a symmetric non-singular 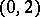 -tensor, and consequently
-tensor, and consequently 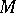 equipped with this metric is a Riemannian manifold. The inverse of the matrix
equipped with this metric is a Riemannian manifold. The inverse of the matrix 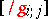 will be denoted by
will be denoted by 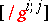 .
.
c) For 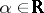 the collection of arrays
the collection of arrays 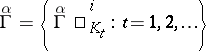 , where
, where
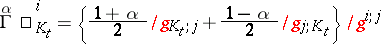 |
is a connection string, i.e. 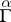 satisfies the transformation law
satisfies the transformation law
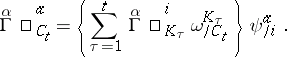 |
In particular, 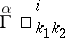 is the (upper) Christoffel symbol of a torsion-free affine connection, the so-called
is the (upper) Christoffel symbol of a torsion-free affine connection, the so-called 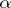 -connection,
-connection, 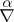 corresponding to the yoke
corresponding to the yoke  .
.
The expected and observed 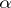 -geometries, see [a1] and [a2], are those corresponding to the expected and observed likelihood yokes, respectively.
-geometries, see [a1] and [a2], are those corresponding to the expected and observed likelihood yokes, respectively.
d) For 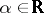 there exists a sequence of tensors
there exists a sequence of tensors 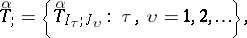 such that
such that 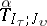 is a covariant tensor of degree
is a covariant tensor of degree 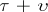 . The quantities
. The quantities 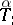 are referred to as the tensorial components of
are referred to as the tensorial components of 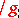 with respect to
with respect to 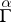 and are obtained by intertwining
and are obtained by intertwining 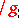 and
and 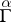 , i.e. determined recursively by the equations
, i.e. determined recursively by the equations
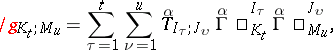 |
where
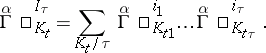 |
In terms of the local coordinates 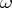 , an invariant Taylor expansion, around
, an invariant Taylor expansion, around 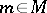 or
or 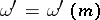 , of a smooth function
, of a smooth function 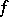 is of the form
is of the form
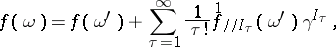 |
where 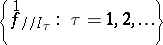 are the tensorial components of the derivatives
are the tensorial components of the derivatives  with respect to the connection string
with respect to the connection string 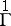 given recursively by
given recursively by
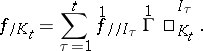 |
Furthermore, 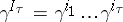 , where
, where 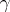 indicates the extended normal coordinates around
indicates the extended normal coordinates around 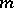 whose components are given by
whose components are given by
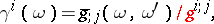 |
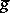 being the normalized yoke corresponding to
being the normalized yoke corresponding to 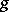 and
and 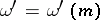 .
.
The Taylor expansion is invariant in the sense that 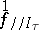 and
and 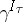 are tensors.
are tensors.
References
| [a1] | S-I. Amari, "Differential-geometrical methods in statistics" , Lecture Notes in Statistics , 28 , Springer (1985) |
| [a2] | O.E. Barndorff-Nielsen, "Likelihood and observed geometries" Ann. Stat. , 14 (1986) pp. 856–873 |
| [a3] | O.E. Barndorff-Nielsen, "Differential geometry and statistics. Some mathematical aspects" Indian J. Math. (Ramanujan Centenary Volume) , 29 (1987) pp. 335–350 |
| [a4] | O.E. Barndorff-Nielsen, P.E Jupp, "Statistics, yokes and symplectic geometry" Ann. Toulouse , to appear (1997) |
| [a5] | P. Blæsild, "Yokes and tensors derived from yokes" Ann. Inst. Statist. Math. , 43 (1991) pp. 95–113 |
Yoke. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Yoke&oldid=17982