Cohomology of Lie algebras
A special case of cohomology of algebras. Let 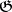 be a Lie algebra over a commutative ring
be a Lie algebra over a commutative ring 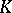 with an identity, and suppose that a left
with an identity, and suppose that a left 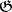 -module
-module  has been given, that is, a
has been given, that is, a 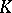 -linear representation of
-linear representation of 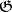 in the
in the 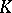 -module
-module 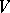 . The
. The 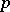 -dimensional cohomology module of the Lie algebra
-dimensional cohomology module of the Lie algebra 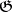 with values in the module
with values in the module 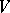 is the module
is the module 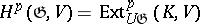 ,
,  where
where 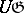 is the universal enveloping algebra of
is the universal enveloping algebra of 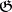 [3]. In other words, the correspondence
[3]. In other words, the correspondence 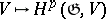 is the
is the 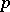 -th right derived functor of the functor
-th right derived functor of the functor 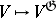 from the category of
from the category of 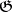 -modules into the category of
-modules into the category of 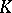 -modules, where
-modules, where 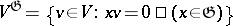 . The functor
. The functor 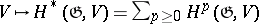 is a cohomology functor (see Homology functor).
is a cohomology functor (see Homology functor).
In small dimensions, the cohomology of Lie algebras can be interpreted as follows. The module 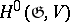 is just
is just 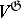 . If
. If 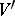 and
and 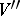 are
are 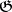 -modules, then
-modules, then 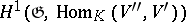 can be identified with the set of equivalence classes of extensions of the
can be identified with the set of equivalence classes of extensions of the 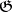 -module
-module 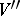 with kernel
with kernel 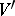 . If
. If 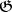 is considered as a
is considered as a 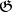 -module with respect to the adjoint representation
-module with respect to the adjoint representation 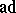 (cf. Adjoint representation of a Lie group), then
(cf. Adjoint representation of a Lie group), then 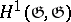 is isomorphic to the quotient module
is isomorphic to the quotient module 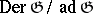 of the module of all derivations (cf. Derivation in a ring) by the submodule of inner derivations. If
of the module of all derivations (cf. Derivation in a ring) by the submodule of inner derivations. If 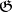 is a free
is a free 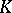 -module (for example, if
-module (for example, if  is a field), then
is a field), then 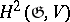 can be identified with the set of equivalence classes of extensions of
can be identified with the set of equivalence classes of extensions of 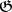 the kernels of which are the Abelian Lie algebra
the kernels of which are the Abelian Lie algebra 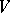 with the given representation of
with the given representation of 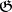 . The module
. The module 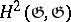 can be interpreted also as the set of infinitesimal deformations of the Lie algebra
can be interpreted also as the set of infinitesimal deformations of the Lie algebra 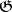 (cf. Deformation).
(cf. Deformation).
The following relation exists between the cohomology of Lie algebras and the cohomology of associative algebras; if 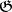 is a free
is a free 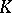 -module and
-module and 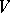 is an arbitrary two-sided
is an arbitrary two-sided 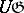 -module, then
-module, then 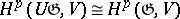 , where the representation of the algebra
, where the representation of the algebra  in
in 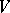 is defined via the formula
is defined via the formula 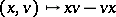 .
.
Another way of defining the cohomology of Lie algebras (see [6], [14]) is by using the cochain complex 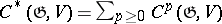 , where
, where 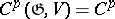 is the module of all skew-symmetric
is the module of all skew-symmetric 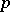 -linear mappings
-linear mappings 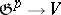 , equipped with the coboundary
, equipped with the coboundary 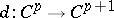 acting by
acting by
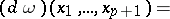 |
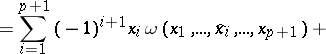 |
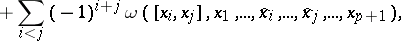 |
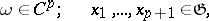 |
where the symbol  means that the relevant argument is deleted. If
means that the relevant argument is deleted. If 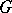 is a free
is a free 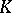 -module, the cohomology modules of this complex are naturally isomorphic to the modules
-module, the cohomology modules of this complex are naturally isomorphic to the modules 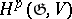 . To every subalgebra
. To every subalgebra 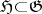 is associated a subcomplex
is associated a subcomplex 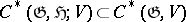 , leading to the relative cohomology
, leading to the relative cohomology 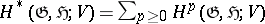 . If
. If 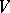 is an algebra over
is an algebra over 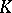 on which
on which 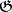 acts by derivations, then a natural multiplication arises in the cohomology modules, turning
acts by derivations, then a natural multiplication arises in the cohomology modules, turning 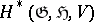 into a graded algebra.
into a graded algebra.
Let  be the Lie algebra (over
be the Lie algebra (over 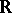 ) of smooth vector fields on a differentiable manifold
) of smooth vector fields on a differentiable manifold 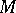 , and let
, and let 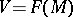 be the space of smooth functions on
be the space of smooth functions on 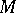 with the natural
with the natural 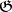 -module structure. The definition of the coboundary in
-module structure. The definition of the coboundary in 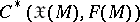 coincides formally with that of exterior differentiation of a differential form. More exactly, the de Rham complex (cf. Differential form) is the subcomplex of
coincides formally with that of exterior differentiation of a differential form. More exactly, the de Rham complex (cf. Differential form) is the subcomplex of 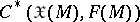 consisting of the cochains that are linear over
consisting of the cochains that are linear over 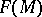 . On the other hand, if
. On the other hand, if 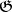 is the Lie algebra of a connected real Lie group
is the Lie algebra of a connected real Lie group 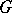 , then the complex
, then the complex 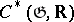 can be identified with the complex of left-invariant differential forms on
can be identified with the complex of left-invariant differential forms on 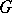 . Analogously, if
. Analogously, if 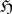 is the subalgebra corresponding to a connected closed subgroup
is the subalgebra corresponding to a connected closed subgroup 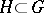 , then
, then 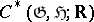 is naturally isomorphic to the complex of
is naturally isomorphic to the complex of 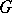 -invariant differential forms on the manifold
-invariant differential forms on the manifold 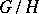 . In particular, if
. In particular, if 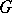 is compact, there follow the isomorphisms of graded algebras:
is compact, there follow the isomorphisms of graded algebras:
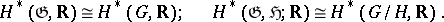 |
Precisely these facts serve as starting-point for the definition of cohomology of Lie algebras. Based on them also is the application of the apparatus of the cohomology theory of Lie algebras to the study of the cohomology of principal bundles and homogeneous spaces (see [8], [14]).
The homology of a Lie algebra 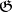 with coefficients in a right
with coefficients in a right 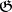 -module
-module 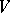 is defined in the dual manner. The
is defined in the dual manner. The 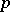 -dimensional homology group is the
-dimensional homology group is the 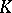 -module
-module 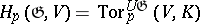 . In particular,
. In particular, 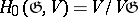 , and if
, and if 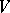 is a trivial
is a trivial  -module,
-module, 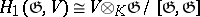 .
.
In calculating the cohomology of a Lie algebra, the following spectral sequences are extensively used; they are often called the Hochschild–Serre spectral sequences. Let 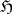 be an ideal of
be an ideal of 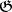 and let
and let 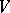 be a
be a 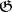 -module. If
-module. If 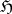 and
and 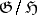 are free
are free 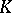 -modules, there exists a spectral sequence
-modules, there exists a spectral sequence 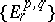 , with
, with 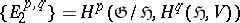 , converging to
, converging to 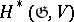 (see [3], [14]). Similar spectral sequences exist for the homology [3]. Further, let
(see [3], [14]). Similar spectral sequences exist for the homology [3]. Further, let 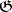 be a finite-dimensional Lie algebra over a field
be a finite-dimensional Lie algebra over a field  of characteristic 0, let
of characteristic 0, let 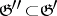 be subalgebras such that
be subalgebras such that 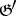 is reductive in
is reductive in 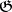 (cf. Lie algebra, reductive), and let
(cf. Lie algebra, reductive), and let 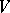 be a semi-simple
be a semi-simple 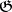 -module. Then there exists a spectral sequence
-module. Then there exists a spectral sequence 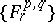 , with
, with  , converging to
, converging to 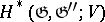 (see [12], [14]).
(see [12], [14]).
The cohomology of finite-dimensional reductive (in particular, semi-simple) Lie algebras over a field of characteristic 0 has been investigated completely. If 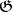 is a finite-dimensional semi-simple Lie algebra over such a field, the following results hold for every finite-dimensional
is a finite-dimensional semi-simple Lie algebra over such a field, the following results hold for every finite-dimensional 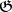 -module
-module 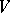 :
:
 |
(Whitehead's lemma). The first of these properties is a sufficient condition for the semi-simplicity of a finite-dimensional algebra 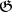 , and is equivalent to the semi-simplicity of all finite-dimensional
, and is equivalent to the semi-simplicity of all finite-dimensional 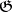 -modules. The second property is equivalent to Levi's theorem (see Levi–Mal'tsev decomposition) for Lie algebras with an Abelian radical [1], [5], [14]. If
-modules. The second property is equivalent to Levi's theorem (see Levi–Mal'tsev decomposition) for Lie algebras with an Abelian radical [1], [5], [14]. If 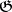 is a reductive Lie algebra,
is a reductive Lie algebra, 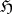 is a subalgebra of it and
is a subalgebra of it and 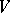 is a finite-dimensional semi-simple module, then
is a finite-dimensional semi-simple module, then 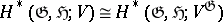 , which reduces the calculation of the cohomology to the case of the trivial
, which reduces the calculation of the cohomology to the case of the trivial 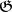 -module
-module  (see [5], [14]). The cohomology algebra
(see [5], [14]). The cohomology algebra  of a reductive Lie algebra
of a reductive Lie algebra 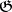 is naturally isomorphic to the algebra
is naturally isomorphic to the algebra  of cochains invariant under
of cochains invariant under 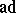 . In this case
. In this case 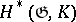 is a Hopf algebra, and thus is an exterior algebra over the space
is a Hopf algebra, and thus is an exterior algebra over the space 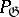 of primitive elements, graded in odd degrees
of primitive elements, graded in odd degrees 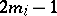 ,
, 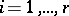 . In particular,
. In particular, 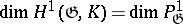 is the dimension of the centre of
is the dimension of the centre of 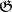 , and
, and 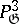 is isomorphic to the space of invariant quadratic forms on
is isomorphic to the space of invariant quadratic forms on 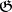 (see [12], [14]). If
(see [12], [14]). If 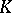 is algebraically closed, then
is algebraically closed, then  is the rank of the algebra
is the rank of the algebra 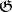 , that is, the dimension of its Cartan subalgebra
, that is, the dimension of its Cartan subalgebra 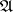 , and
, and 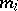 are the degrees of the free generators in the algebra of polynomials over
are the degrees of the free generators in the algebra of polynomials over 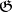 invariant under
invariant under 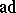 (or in the algebra of polynomials over
(or in the algebra of polynomials over 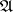 invariant under the Weyl group, which is isomorphic to it). In this case the numbers
invariant under the Weyl group, which is isomorphic to it). In this case the numbers 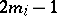 are the dimensions of the primitive cohomology classes of the corresponding compact Lie group. The numbers
are the dimensions of the primitive cohomology classes of the corresponding compact Lie group. The numbers 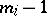 are called the exponents of the Lie algebra
are called the exponents of the Lie algebra 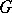 . The homology algebra
. The homology algebra 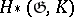 of a reductive Lie algebra
of a reductive Lie algebra 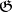 over a field of characteristic 0 is the exterior algebra dual to
over a field of characteristic 0 is the exterior algebra dual to 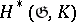 . For any
. For any  -dimensional Lie algebra
-dimensional Lie algebra 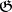 , an analogue of Poincaré duality holds:
, an analogue of Poincaré duality holds:
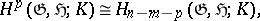 |
where 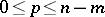 and
and 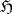 is an arbitrary
is an arbitrary 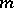 -dimensional reductive subalgebra of
-dimensional reductive subalgebra of 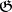 (see [14], ).
(see [14], ).
Only a few general assertions are known about the cohomology of solvable Lie algebras. For example, let 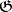 be a finite-dimensional nilpotent Lie algebra over an infinite field and let
be a finite-dimensional nilpotent Lie algebra over an infinite field and let 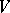 be a finite-dimensional
be a finite-dimensional 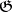 -module. Then
-module. Then 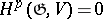 for all
for all 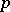 if
if  has no trivial
has no trivial 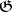 -submodules, and
-submodules, and 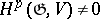 for
for 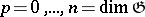 , and
, and 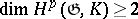 for
for  if such a
if such a 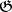 -submodule does exist (see [7]). The groups
-submodule does exist (see [7]). The groups 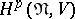 , are well-studied in the case that
, are well-studied in the case that 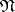 is the nilpotent radical of the parabolic subalgebra
is the nilpotent radical of the parabolic subalgebra 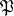 of some semi-simple Lie algebra
of some semi-simple Lie algebra 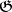 over an algebraically closed field of characteristic 0, and the representation of
over an algebraically closed field of characteristic 0, and the representation of 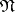 in
in 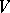 is the restriction of some representation of
is the restriction of some representation of  in
in 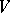 (see [11]). These cohomology groups are closely related to those of the complex homogeneous space
(see [11]). These cohomology groups are closely related to those of the complex homogeneous space 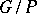 corresponding to the pair
corresponding to the pair 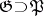 , with values in sheaves of germs of holomorphic sections of homogeneous vector bundles over
, with values in sheaves of germs of holomorphic sections of homogeneous vector bundles over 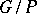 . In the calculation of the cohomology of a finite-dimensional non-semi-simple Lie algebra over a field of characteristic 0, one uses the formula
. In the calculation of the cohomology of a finite-dimensional non-semi-simple Lie algebra over a field of characteristic 0, one uses the formula
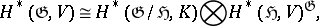 |
where 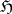 is an ideal in
is an ideal in 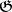 such that
such that 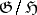 is semi-simple [14].
is semi-simple [14].
In some cases, a relation can be established between the cohomology of Lie algebras and the cohomology of groups. Let 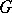 be a connected real Lie group, let
be a connected real Lie group, let 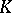 be a maximal compact subgroup of it, let
be a maximal compact subgroup of it, let 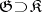 be their Lie algebras, and let
be their Lie algebras, and let  be a finite-dimensional smooth
be a finite-dimensional smooth 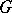 -module. If a natural
-module. If a natural  -module structure is defined on
-module structure is defined on 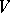 , then
, then 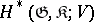 is isomorphic to the cohomology of
is isomorphic to the cohomology of 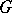 (as an abstract group), calculated by means of continuous cochains [10]. On the other hand, let
(as an abstract group), calculated by means of continuous cochains [10]. On the other hand, let  be the Lie algebra of a simply-connected solvable Lie group
be the Lie algebra of a simply-connected solvable Lie group 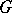 , let
, let 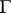 be a lattice in
be a lattice in 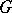 and let
and let 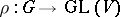 be a smooth finite-dimensional linear representation. If
be a smooth finite-dimensional linear representation. If 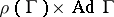 is Zariski dense in the algebraic closure of
is Zariski dense in the algebraic closure of 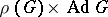 , then
, then 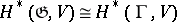 (see [4]). In general,
(see [4]). In general, 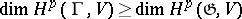
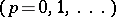 . For nilpotent
. For nilpotent 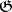 it suffices to require that
it suffices to require that 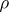 be unipotent. If the lattice
be unipotent. If the lattice 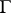 in a simply-connected Lie group
in a simply-connected Lie group 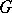 is such that
is such that 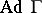 is dense in the algebraic closure of the group
is dense in the algebraic closure of the group 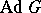 (for example, if
(for example, if 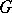 is nilpotent), then
is nilpotent), then 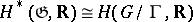 .
.
In recent years there has been a systematic study of the cohomology of certain infinite-dimensional Lie algebras. Among these are the algebra 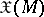 of vector fields on a differentiable manifold
of vector fields on a differentiable manifold 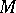 , the Lie algebra of formal vector fields, the subalgebras of these algebras consisting of the gradient-free, Hamiltonian or canonical vector fields (see [2], [13]), and also certain classical Banach Lie algebras.
, the Lie algebra of formal vector fields, the subalgebras of these algebras consisting of the gradient-free, Hamiltonian or canonical vector fields (see [2], [13]), and also certain classical Banach Lie algebras.
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [2] | D.B. [D.B. Fuks] Fuchs, "Cohomology of infinite-dimensional Lie algebras" , Plenum (1986) (Translated from Russian) |
| [3] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [4] | M.S. Raghunathan, "Discrete subgroups of Lie groups" , Springer (1972) |
| [5] | , Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Ecole Norm. Sup. (1955) |
| [6] | C. Chevalley, S. Eilenberg, "Cohomology theory of Lie groups and Lie algebras" Trans. Amer. Math. Soc. , 63 (1948) pp. 85–124 |
| [7] | J. Dixmier, "Cohomologie des algèbres de Lie nilpotents" Acta Sci. Mat. Szeged , 16 : 3–4 (1955) pp. 246–250 |
| [8] | W. Greub, S. Halperin, R. Vanstone, "Connections, curvature and cohomology. Cohomology of principal bundles and homogeneous spaces" , 3 , Acad. Press (1975) |
| [9] | P. de la Harpe, "Classical Banach–Lie algebras and Banach–Lie groups of operators in Hilbert space" , Springer (1972) |
| [10] | G. Hochschild, G.D. Mostow, "Cohomology of Lie groups" Ill. J. Math. , 6 : 3 (1962) pp. 367–401 |
| [11] | B. Kostant, "Lie algebra cohomology and the generalized Borel–Weil theorem" Ann. Math. , 74 : 2 (1961) pp. 329–387 |
| [12] | J.L. Koszul, "Homologie et cohomologie des algèbres de Lie" Bull. Soc. Math. France , 78 (1950) pp. 65–127 |
| [13] | A. Lichnerowicz, "Cohomologie 1-différentiables des algèbres de Lie attaché à une variété symplectique ou de contact" J. Math. Pures Appl. , 53 : 4 (1974) pp. 459–483 |
| [14] | A. Verona, "Introducere in coomologia algebrelor Lie" , Bucharest (1974) |
| [15] | A. Guichardet, "Cohomologie des groupes topologiques et des algèbres de Lie" , F. Nathan (1980) |
Comments
The subcomplex  of relative cochains is defined by
of relative cochains is defined by 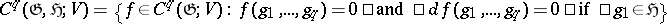 . Equivalently,
. Equivalently, 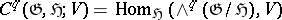 .
.
There is a generalization of the Poincaré duality result as follows. Let 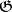 be free of finite dimension over
be free of finite dimension over 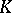 . For a
. For a 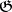 -module
-module 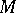 let
let  be the dual Lie module defined by
be the dual Lie module defined by 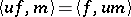 for
for 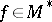 ,
, 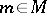 ,
, 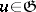 , and let
, and let 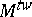 be the
be the 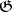 -module with underlying
-module with underlying 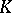 -module
-module 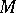 but with the
but with the 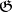 -action changed to
-action changed to 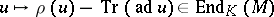 , where
, where 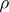 is the action of
is the action of 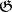 on
on 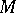 . Then there is a canonical isomorphism, [a1],
. Then there is a canonical isomorphism, [a1],
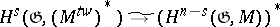 |
of 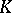 -modules where
-modules where 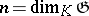 . Note that if
. Note that if 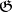 is semi-simple then
is semi-simple then 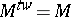 .
.
References
| [a1] | M. Hazewinkel, "A duality theorem for the cohomology of Lie algebras" Math. USSR-Sb. , 12 (1970) pp. 638–644 Mat. Sb. , 83 (125) (1970) pp. 639–644 |
Cohomology of Lie algebras. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cohomology_of_Lie_algebras&oldid=17977