Tangent flow

A flow in the space of orthonormal -frames of an -dimensional Riemannian manifold , having the following property. Let be an arbitrary trajectory of the flow; by definition of the spac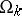e , is some -frame at some point (that is, in the tangent space to at this point). It is required that (a variant: it is required that the moving frame of the parametrized curve 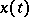in 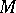has as its first 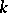vectors precisely ). To obtain interesting results on tangent flows it is necessary to impose various extra conditions. The results obtained generalize certain of the properties of a geodesic flow (which is a particular case of a tangent flow, when and the covariant derivative ). See [1], [2].

Various types of flow in the tangent space to some manifold (or, if it is supposed that is endowed with a Riemannian or a Finsler metric, in the space of unit tangent vectors) were sometimes called tangent flows. For example, a spray (generally, a system of equations of the second order) on and the variational equation of a flow on 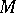were called tangent flows. But this terminology did not achieve wide application. More customary terminology has since been used.

References

[1]	V.I. Arnol'd, "Some remarks on flows of line elements and frames" Soviet Math. Dokl. , 2 (1961) pp. 562–564 Dokl. Akad. Nauk SSSR , 138 : 2 (1961) pp. 255–257
[2]	V.I. Arnol'd, "Remarks on winding numbers" Sibirsk. Mat. Zh. , 2 : 6 (1961) pp. 807–813 (In Russian)