Non-smoothable manifold
A piecewise-linear or topological manifold that does not admit a smooth structure.
A smoothing of a piecewise-linear manifold 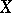 is a piecewise-linear isomorphism
is a piecewise-linear isomorphism 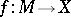 , where
, where 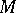 is a smooth manifold. Manifolds that do not admit smoothings are said to be non-smoothable. With certain modifications this is also applicable to topological manifolds.
is a smooth manifold. Manifolds that do not admit smoothings are said to be non-smoothable. With certain modifications this is also applicable to topological manifolds.
Example of a non-smoothable manifold. Let 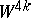 ,
, 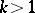 , be a
, be a 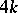 -dimensional Milnor manifold (see Dendritic manifold). In particular,
-dimensional Milnor manifold (see Dendritic manifold). In particular, 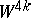 is parallelizable, its signature is 8, and its boundary
is parallelizable, its signature is 8, and its boundary 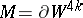 is homotopy equivalent to the sphere
is homotopy equivalent to the sphere 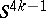 . Glueing to
. Glueing to 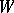 a cone
a cone 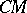 over
over 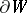 leads to the space
leads to the space 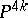 . Since
. Since 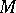 is a piecewise-linear sphere (see generalized Poincaré conjecture),
is a piecewise-linear sphere (see generalized Poincaré conjecture), 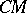 is a piecewise-linear disc, so that
is a piecewise-linear disc, so that 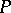 is a piecewise-linear manifold. On the other hand,
is a piecewise-linear manifold. On the other hand, 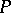 is non-smoothable, since its signature is 8, while that of an almost-parallelizable (that is, parallelizable after removing a point)
is non-smoothable, since its signature is 8, while that of an almost-parallelizable (that is, parallelizable after removing a point) 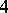 -dimensional manifold is a multiple of a number
-dimensional manifold is a multiple of a number 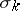 that grows exponentially with
that grows exponentially with 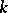 . The manifold
. The manifold 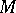 is not diffeomorphic to the sphere
is not diffeomorphic to the sphere 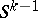 , that is,
, that is, 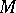 is a Milnor sphere.
is a Milnor sphere.
A criterion for a piecewise-linear manifold to be smoothable is as follows. Let 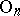 be the orthogonal group and let
be the orthogonal group and let 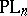 be the group of piecewise-linear homeomorphisms of
be the group of piecewise-linear homeomorphisms of 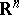 preserving the origin (see Piecewise-linear topology). The inclusion
preserving the origin (see Piecewise-linear topology). The inclusion 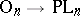 induces a fibration
induces a fibration 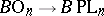 , where
, where 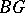 is the classifying space of a group
is the classifying space of a group 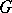 . As
. As 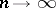 there results a fibration
there results a fibration 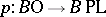 , the fibre of which is denoted by
, the fibre of which is denoted by 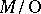 . A piecewise-linear manifold
. A piecewise-linear manifold 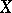 has a linear stable normal bundle
has a linear stable normal bundle  with classifying mapping
with classifying mapping  . If
. If 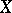 is smoothable (or smooth), then it has a stable normal bundle
is smoothable (or smooth), then it has a stable normal bundle 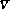 with classifying mapping
with classifying mapping 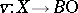 and
and 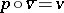 . This condition is also sufficient, that is, a closed piecewise-linear manifold
. This condition is also sufficient, that is, a closed piecewise-linear manifold 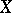 is smoothable if and only if its piecewise-linear stable normal bundle admits a vector reduction, that is, if the mapping
is smoothable if and only if its piecewise-linear stable normal bundle admits a vector reduction, that is, if the mapping 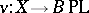 can be "lifted" to
can be "lifted" to 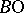 (there is a
(there is a 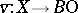 such that
such that 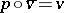 ).
).
Two smoothings 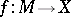 and
and 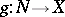 are said to be equivalent if there is a diffeomorphism
are said to be equivalent if there is a diffeomorphism 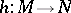 such that
such that 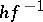 is piecewise differentiably isotopic to
is piecewise differentiably isotopic to 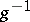 (see Structure on a manifold). The sets
(see Structure on a manifold). The sets 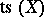 of equivalence classes of smoothings are in a natural one-to-one correspondence with the fibre-wise homotopy classes of liftings
of equivalence classes of smoothings are in a natural one-to-one correspondence with the fibre-wise homotopy classes of liftings  of
of 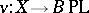 . In other words, when
. In other words, when 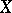 is smoothable,
is smoothable, 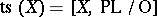 .
.
References
| [1] | M. Kervaire, "A manifold which does not admit any differentiable structure" Comment. Math. Helv. , 34 (1960) pp. 257–270 |
| [2] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) |
Comments
References
| [a1] | M.W. Hirsch, B. Mazur, "Smoothings of piecewise linear manifolds" , Princeton Univ. Press (1974) |
| [a2] | L.C. Siebenmann, "Topological manifolds" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 2 , Gauthier-Villars (1971) pp. 133–163 |
| [a3] | S. Smale, "The generalized Poincaré conjecture in higher dimensions" Bull. Amer. Math. Soc. , 66 (1960) pp. 373–375 |
Non-smoothable manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-smoothable_manifold&oldid=17941