Relativistic hydrodynamics, mathematical problems in

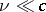Problems for a system of equations that describes the flow of a fluid with velocities approaching the velocity of light , as well as its interaction with strong gravitational fields. In the extreme case of low velocities and weak gravitational fields 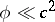, where 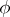is the gravitational potential, these problems are reduced to mathematical problems in hydrodynamics (cf. Hydrodynamics, mathematical problems in). The system of equations of relativistic hydrodynamics is formed by putting the covariant divergences of the energy-momentum tensor and the density vector of matter flow equal zero:

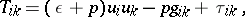(1)

(2)

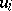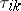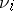where , and are the energy density, the pressure and the density of the number of particles in the system of reference that is at rest with respect to the fluid element in question, is the metric tensor, is the four-dimensional velocity, and and are the parts of the energy-momentum tensor and the vector of matter flow describing the effects associated with viscosity (see [1]).

The following is an example of solutions to mathematical problems in relativistic hydrodynamics: when sound is propagated in a matter with an ultra-relativistic equation of state 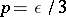, then, for a perturbation of the pressure or the energy density, the wave equation with velocity of sound 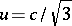is obtained.

The mathematical problems in relativistic hydrodynamics arise, e.g., in the examination of processes occurring in the vicinity of stars that possess strong gravitational fields (neutron stars and so-called "black holes" ), and in an expanding Universe filled with radiation and matter.

References

[1]	L.D. Landau, E.M. Lifshitz, "Fluid mechanics" , Pergamon (1959) (Translated from Russian)
[2]	Ya.B. Zel'dovich, I.D. Novikov, "Relativistic astrophysics" , 1. Stars and relativity , Chicago (1971) (Translated from Russian)
[3]	Ya.B. Zel'dovich, I.D. Novikov, "Relativistic astrophysics" , 2. Structure and evolution of the Universe , Chicago (1983) (Translated from Russian)
[4]	C.W. Misner, K.S. Thorne, J.A. Wheeler, "Gravitation" , Freeman (1973) pp. Chapt. 22

References

[a1]	A. Lichnerowicz, "Relativistic hydrodynamics and magnetohydrodynamics" , Benjamin (1967)
[a2]	A. Anile (ed.) Y. Choquet-Bruhat (ed.) , Relativistic fluid dynamics , Lect. notes in math. , 1385 , Springer (1989)