K-contact-flow
A contact form on a smooth  -dimensional manifold
-dimensional manifold  is a
is a  -form
-form  such that
such that  is everywhere non-zero. The pair
is everywhere non-zero. The pair  is called a contact manifold. See also Contact structure.
is called a contact manifold. See also Contact structure.
A contact manifold  carries a distinguished vector field
carries a distinguished vector field  , called the characteristic vector field or Reeb field, which is uniquely determined by the following equations:
, called the characteristic vector field or Reeb field, which is uniquely determined by the following equations:  and
and  for all vector fields
for all vector fields  . The flow
. The flow 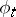 generated by
generated by  (when it is complete) is called the contact flow. Sometimes the name "contact flow" is used for the
(when it is complete) is called the contact flow. Sometimes the name "contact flow" is used for the  -dimensional foliation
-dimensional foliation  consisting of the unparametrized orbits of
consisting of the unparametrized orbits of 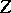 , [a5].
, [a5].
If the flow  is a Riemannian foliation in the sense of Reinhart–Molino [a7], i.e., if there is a holonomy-invariant transverse metric for
is a Riemannian foliation in the sense of Reinhart–Molino [a7], i.e., if there is a holonomy-invariant transverse metric for 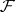 , then
, then  is called a
is called a 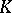 -contact flow, and the pair
-contact flow, and the pair 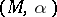 is called a
is called a  -contact manifold. This definition is equivalent to requiring that the flow
-contact manifold. This definition is equivalent to requiring that the flow  of
of  is a
is a 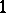 -parameter group of isometries for some contact metric (a Riemannian metric
-parameter group of isometries for some contact metric (a Riemannian metric 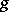 such that there exists an endomorphism
such that there exists an endomorphism 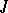 of the tangent bundle
of the tangent bundle 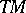 such that
such that  ,
,  ,
,  , and
, and 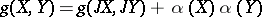 for all vector fields
for all vector fields 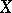 and
and  on
on  ). If one has in addition
). If one has in addition 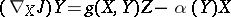 , where
, where  is the Levi-Civita connection of
is the Levi-Civita connection of 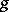 , then one says that
, then one says that 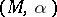 is a Sasakian manifold, [a4], [a12].
is a Sasakian manifold, [a4], [a12].
As a consequence of the Meyer–Steenrod theorem [a6], a 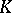 -contact flow
-contact flow 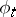 on a compact
on a compact  -dimensional manifold is almost periodic: the closure of
-dimensional manifold is almost periodic: the closure of 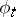 in the isometry group of
in the isometry group of 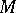 (of the associated contact metric) is a torus
(of the associated contact metric) is a torus  , of dimension
, of dimension 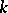 in between
in between 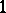 and
and 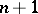 , which acts on
, which acts on 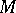 while preserving the contact form
while preserving the contact form 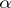 , [a3]. The "completely integrable" case
, [a3]. The "completely integrable" case 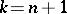 has been studied in [a2]: these structures are determined by the image of their contact moment mapping.
has been studied in [a2]: these structures are determined by the image of their contact moment mapping.
The existence of 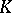 -contact flows poses restrictions on the topology of the manifold. For instance, since a
-contact flows poses restrictions on the topology of the manifold. For instance, since a  -contact flow can be approximated by a periodic
-contact flow can be approximated by a periodic  -contact flow, only Seifert fibred compact manifolds can carry a
-contact flow, only Seifert fibred compact manifolds can carry a 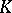 -contact flow. Another example of a restriction is the Tachibana theorem, asserting that the first Betti number of a compact Sasakian manifold is either zero or even, [a9]. This shows that no torus
-contact flow. Another example of a restriction is the Tachibana theorem, asserting that the first Betti number of a compact Sasakian manifold is either zero or even, [a9]. This shows that no torus  can carry a Sasakian structure. Actually, P. Rukimbira [a8] showed that no torus can carry a
can carry a Sasakian structure. Actually, P. Rukimbira [a8] showed that no torus can carry a 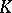 -contact flow.
-contact flow.
A. Weinstein [a11] has conjectured that the contact flow of a compact contact manifold has at least one periodic orbit. Despite important breakthroughs (including [a10]), this conjecture is not quite settled at present (1996). However, it is known that  -contact flows on compact manifolds have at least two periodic orbits [a3].
-contact flows on compact manifolds have at least two periodic orbits [a3].
Examples of 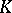 -contact manifolds include the contact manifolds
-contact manifolds include the contact manifolds  with a periodic contact flow
with a periodic contact flow  (these include the regular contact manifolds), such as the sphere
(these include the regular contact manifolds), such as the sphere 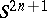 equipped with the contact form
equipped with the contact form 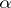 that is the restriction to
that is the restriction to 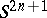 of the
of the 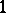 -form
-form
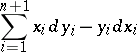 |
on 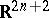 . More generally, compact contact hypersurfaces (in the sense of M. Okumura) [a1] in Kähler manifolds of constant positive holomorphic sectional curvature carry
. More generally, compact contact hypersurfaces (in the sense of M. Okumura) [a1] in Kähler manifolds of constant positive holomorphic sectional curvature carry 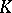 -contact flows. A large set of examples is provided by the Brieskorn manifolds: In [a12] it is shown that every Brieskorn manifold admits many Sasakian structures, hence carries many
-contact flows. A large set of examples is provided by the Brieskorn manifolds: In [a12] it is shown that every Brieskorn manifold admits many Sasakian structures, hence carries many  -contact flows.
-contact flows.
References
| [a1] | A. Banyaga, "On characteristics of hypersurfaces in symplectic manifolds" , Proc. Symp. Pure Math. , 54 , Amer. Math. Soc. (1993) pp. 9–17 |
| [a2] | A. Banyaga, P. Molino, "Complete integrability in contact geometry" , Memoirs , Amer. Math. Soc. (submitted) |
| [a3] | A. Banyaga, P. Rukimbira, "On characteristics of circle invariant presymplectic forms" Proc. Amer. Math. Soc. , 123 (1995) pp. 3901–3906 |
| [a4] | D.E. Blair, "Contact manifolds in Riemannian geometry" , Lecture Notes in Mathematics , 509 , Springer (1976) |
| [a5] | Y. Carrière, "Flots riemanniens" Astérisque , 116 (1982) pp. 31–52 |
| [a6] | S.B. Meyer, N.E. Steenrod, "The group of isometries of a Riemannian manifold" Ann. of Math. , 40 (1939) pp. 400–416 |
| [a7] | P. Molino, "Riemannian foliations" , Progress in Math. , Birkhäuser (1984) |
| [a8] | P. Rukimbira, "Some remarks on 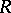 -contact flows" Ann. Global Anal. and Geom. , 11 (1993) pp. 165–171 -contact flows" Ann. Global Anal. and Geom. , 11 (1993) pp. 165–171 |
| [a9] | S. Tachibana, "On harmonic tensors in compact sasakian spaces" Tohoku Math. J. , 17 (1965) pp. 271–284 |
| [a10] | C. Viterbo, "A proof of the Weinstein conjecture for 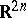 " Ann. Inst. H. Poincaré. Anal. Non-Lin. , 4 (1987) pp. 337–356 " Ann. Inst. H. Poincaré. Anal. Non-Lin. , 4 (1987) pp. 337–356 |
| [a11] | A. Weinstein, "On the hypothesis of Rabinowicz' periodic orbit theorem" J. Diff. Geom. , 33 (1978) pp. 353–358 |
| [a12] | K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984) |
K-contact-flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K-contact-flow&oldid=17811