Markov criterion
From Encyclopedia of Mathematics
for best integral approximation
A theorem which in some cases enables one to give effectively the polynomial and the error of best integral approximation of a function  . It was established by A.A. Markov in 1898 (see [1]). Let
. It was established by A.A. Markov in 1898 (see [1]). Let 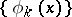 ,
, 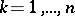 , be a system of linearly independent functions continuous on the interval
, be a system of linearly independent functions continuous on the interval 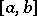 , and let the continuous function
, and let the continuous function 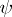 change sign at the points
change sign at the points  in
in 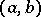 and be such that
and be such that
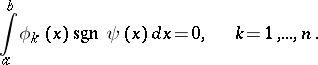 |
If the polynomial
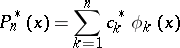 |
has the property that the difference 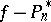 changes sign at the points
changes sign at the points  , and only at those points, then
, and only at those points, then 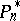 is the polynomial of best integral approximation to
is the polynomial of best integral approximation to 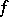 and
and
 |
 |
For the system  on
on 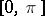 ,
, 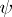 can be taken to be
can be taken to be 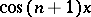 ; for the system
; for the system 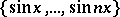 ,
, 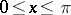 ,
, 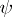 can be taken to be
can be taken to be  ; and for the system
; and for the system 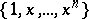 ,
, 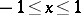 , one can take
, one can take 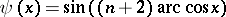 .
.
References
| [1] | A.A. Markov, "Selected works" , Moscow-Leningrad (1948) (In Russian) |
| [2] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
| [3] | I.K. Daugavet, "Introduction to the theory of approximation of functions" , Leningrad (1977) (In Russian) |
Comments
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) |
| [a2] | M.W. Müller, "Approximationstheorie" , Akad. Verlagsgesellschaft (1978) |
| [a3] | J.R. Rice, "The approximation of functions" , 1. Linear theory , Addison-Wesley (1964) |
How to Cite This Entry:
Markov criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_criterion&oldid=17793
Markov criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_criterion&oldid=17793
This article was adapted from an original article by N.P. KorneichukV.P. Motornyi (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article