Binormal
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
The straight line passing through a point 
of a curve 
perpendicular to the osculating plane to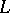 
at 
. If 
is a parametrization of 
, then the vector equation of the binormal at 
corresponding to the value 
of the parameter 
has the form
 |
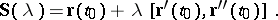Comments
This definition holds for space curves for which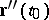 
does not depend linearly on 
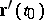, i.e. the curvature should not vanish.
For curves in a higher-dimensional Euclidean space, the binormal is generated by the second normal vector in the Frénet frame (cf. Frénet trihedron), which is perpendicular to the plane spanned by 
and 
and depends linearly on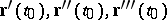 
(cf. [a1]).
References
| [a1] | M. Spivak, "A comprehensive introduction to differential geometry" , 2 , Publish or Perish (1970) pp. 1–5 |
How to Cite This Entry:
Binormal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binormal&oldid=17792
Binormal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binormal&oldid=17792
This article was adapted from an original article by E.V. Shikin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article