Boundary value problem, ordinary differential equations

The problem of finding a solution to an equation

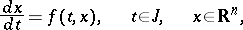(1)

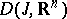lying in a given subset of the space of functions depending on 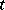that are absolutely continuous on 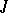and that assume values in :

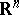(2)

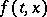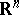It is assumed that is a function defined on with values in and satisfying the Carathéodory conditions; 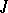is an interval on the real line .

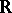1) The boundary value problem (1), (2) is said to be linear if

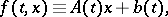where the functions 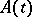and are summable on every compact interval in 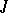and the set 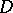is a linear manifold in 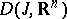. In particular, one might have

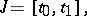where is a function of bounded variation. A linear boundary value problem gives rise to a linear operator

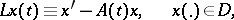the eigen values of which are precisely those values of the parameter 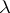for which the homogeneous boundary value problem

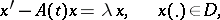has non-trivial solutions. These non-trivial solutions are the eigen functions of the operator 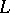. If the inverse operator exists and has an integral representation

then is called a Green function.

2) Let , let be almost-periodic in 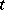uniformly in on every compact subset of 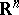and let 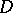be the set of almost-periodic functions in 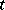that are absolutely continuous on 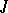. Then problem (1), (2) is known as the problem of almost-periodic solutions.

3) In control theory one considers boundary value problems with a functional parameter: a control. For example, consider the equation

(3)

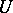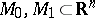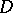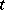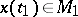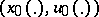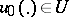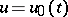with set of admissible controls and two sets . Let be the set of absolutely continuous functions in such that , . The boundary value problem is to find a pair such that and the solution of equation (3) at satisfies the condition .

4) There is a wide range of diverse necessary and sufficient conditions for the existence and uniqueness of solutions to various boundary value problems, and of methods for constructing an approximate solution (see [4]–[7]). For example, consider the problem

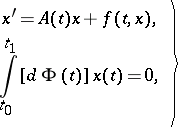(4)

in which

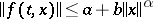for certain constants 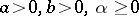. Suppose that the homogeneous problem

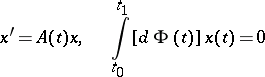(5)

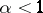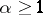is regular, i.e. its only solution is the trivial one. Then problem (4) has at least one solution, provided either , or and 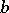is sufficiently small. It is fairly complicated to determine whether problem (5) is regular. However, the linear (scalar) boundary value problem

for example, is regular if whenever 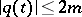there exists a such that

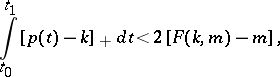where

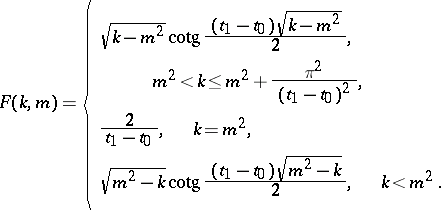References

[1]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)
[2]	M.A. Krasnosel'skii, V.Sh. Burd, Yu.S. Kolesov, "Nonlinear almost-periodic oscillations" , Wiley (1973) (Translated from Russian)
[3]	L.S. Pontryagin, V.G. Boltayanskii, R.V. Gamkrelidze, E.F. Mishchenko, "The mathematical theory of optimal processes" , Interscience (1962) (Translated from Russian)
[4]	N.N. Krasovskii, "Theory of control of motion. Linear systems" , Moscow (1968) (In Russian)
[5]	V.I. Zubov, "Lectures in control theory" , Moscow (1975) (In Russian)
[6]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971)
[7]	I.T. Kiguradze, "Some singular boundary value problems for ordinary differential equations" , Tbilisi (1975) (In Russian)

References

[a1]	M. Braun, "Differential equations and their applications" , Springer (1975)
[a2]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) pp. §§3.6, 3.51, 4.7, A.5
[a3]	L.K. Jackson, "Boundary value problems for ordinary differential equations" J.K. Hale (ed.) , Studies in ordinary differential equations , Math. Assoc. Amer. (1977) pp. 93–127