Dirichlet series for an analytic almost-periodic function
A series of the type
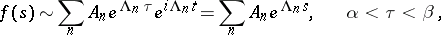 | (*) |
representing in the strip 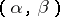 ,
, 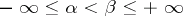 , the complete Fourier series of the analytic, regular almost-periodic function
, the complete Fourier series of the analytic, regular almost-periodic function 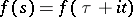 , defined on the union of straight lines
, defined on the union of straight lines 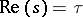 (cf. Almost-periodic analytic function).
(cf. Almost-periodic analytic function).
To two different almost-periodic functions in the same strip correspond two different Dirichlet series. In the case of a 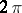 -periodic function the series (*) becomes a Laurent series. The numbers
-periodic function the series (*) becomes a Laurent series. The numbers 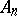 and
and 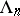 are known, respectively, as the Dirichlet coefficients and exponents. Unlike for classical Dirichlet series, the set of real exponents
are known, respectively, as the Dirichlet coefficients and exponents. Unlike for classical Dirichlet series, the set of real exponents 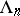 in (*) may have finite limit points and may even be everywhere dense. If all Dirichlet exponents have the same sign, for example, if
in (*) may have finite limit points and may even be everywhere dense. If all Dirichlet exponents have the same sign, for example, if 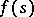 is an almost-periodic function in a strip
is an almost-periodic function in a strip 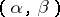 and if in (*)
and if in (*) 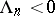 , then
, then 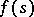 is an almost-periodic function in the strip
is an almost-periodic function in the strip 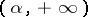 , and
, and 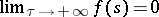 uniformly with respect to
uniformly with respect to 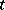 . A similar theorem is valid for positive Dirichlet exponents [2]. If
. A similar theorem is valid for positive Dirichlet exponents [2]. If 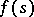 is an almost-periodic function in a strip
is an almost-periodic function in a strip 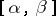 and if the indefinite integral of
and if the indefinite integral of 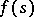 in the strip
in the strip 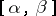 is bounded, then the series
is bounded, then the series
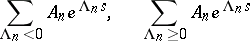 |
are the Dirichlet series of two functions 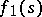 and
and 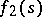 which are almost-periodic in every strip
which are almost-periodic in every strip 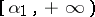 ,
, 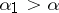 or, respectively,
or, respectively, 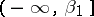 ,
, 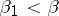 .
.
References
| [1] | H. Bohr, "Almost periodic functions" , Chelsea, reprint (1947) (Translated from German) |
| [2] | B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian) |
Comments
References
| [a1] | A.S. Besicovitch, "Almost periodic functions" , Cambridge Univ. Press (1932) |
| [a2] | C. Corduneanu, "Almost periodic functions" , Wiley (1968) (Translated from Rumanian) |
Dirichlet series for an analytic almost-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_series_for_an_analytic_almost-periodic_function&oldid=17761