Hypercentre
From Encyclopedia of Mathematics
A member 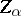 of the upper central series of a group
of the upper central series of a group 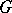 . The first hypercentre
. The first hypercentre 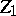 is the centre of the group (cf. Centre of a group); if all
is the centre of the group (cf. Centre of a group); if all 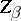 ,
, 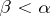 , are known, then
, are known, then 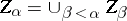 if
if 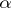 is a limit ordinal number;
is a limit ordinal number; 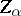 is the complete pre-image of the centre of the quotient group
is the complete pre-image of the centre of the quotient group 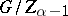 if
if 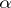 is a non-limit ordinal number. The hypercentres of a group are locally nilpotent.
is a non-limit ordinal number. The hypercentres of a group are locally nilpotent.
Comments
References
| [a1] | D.J.S. Robinson, "Finiteness condition and generalized soluble groups" , 1–2 , Springer (1972) |
How to Cite This Entry:
Hypercentre. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypercentre&oldid=17756
Hypercentre. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypercentre&oldid=17756
This article was adapted from an original article by V.M. Kopytov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article