S-duality
stationary duality, Spanier duality
A duality in homotopy theory which exists (in the absence of restrictions imposed on the dimensions of spaces) for the analogues of ordinary homotopy and cohomotopy groups in the suspension category — for the 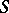 -homotopy and
-homotopy and 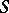 -cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or
-cohomotopy groups or stationary homotopy and cohomotopy groups, forming extra-ordinary (generalized) homology and cohomology theories. A suspension category, or 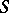 -category, is a category whose objects are topological spaces
-category, is a category whose objects are topological spaces 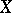 , while its morphisms are classes
, while its morphisms are classes  of
of 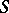 -homotopic mappings
-homotopic mappings 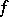 from a
from a 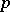 -fold suspension
-fold suspension 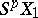 into
into 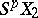 ,
, 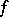 and
and 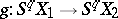 being considered as
being considered as 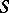 -homotopic if there exists an
-homotopic if there exists an 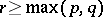 such that the suspensions
such that the suspensions 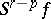 and
and  are homotopic in the ordinary sense. The set
are homotopic in the ordinary sense. The set 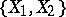 of such classes, which are known as
of such classes, which are known as 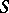 -mappings, constitutes an Abelian group with respect to the so-called track addition [1], [2], [4], [5]. The group
-mappings, constitutes an Abelian group with respect to the so-called track addition [1], [2], [4], [5]. The group 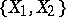 is the limit of the direct spectrum of the sets
is the limit of the direct spectrum of the sets 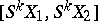 of ordinary homotopy classes with suspension mappings as projections; if
of ordinary homotopy classes with suspension mappings as projections; if 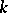 is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism
is sufficiently large, it is a group spectrum with homomorphisms. There exists an isomorphism 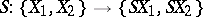 in which the corresponding elements are represented by one and the same mapping
in which the corresponding elements are represented by one and the same mapping 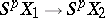 ,
, 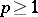 . The
. The  -dual polyhedron of the polyhedron
-dual polyhedron of the polyhedron 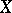 in a sphere
in a sphere 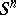 is an arbitrary polyhedron
is an arbitrary polyhedron 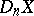 in
in 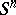 which is an
which is an 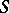 -deformation retract of the complement
-deformation retract of the complement 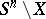 , i.e. the morphism corresponding to the imbedding
, i.e. the morphism corresponding to the imbedding 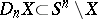 is an
is an 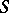 -equivalence. The polyhedron
-equivalence. The polyhedron 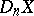 exists for all
exists for all 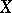 , and
, and  may be considered as
may be considered as 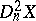 .
.
For any polyhedra 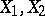 and any polyhedra
and any polyhedra 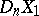 and
and 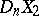 which are dual to them, there exists a unique mapping
which are dual to them, there exists a unique mapping
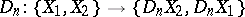 |
satisfying the following conditions:
a) It is an involutory contravariant functorial isomorphism, i.e. 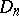 is a homomorphism such that if
is a homomorphism such that if
 |
then
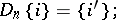 |
if
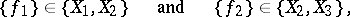 |
then
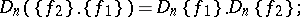 |
if 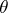 is an element of
is an element of 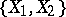 or of
or of 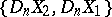 , then
, then 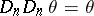 .
.
b) The following relations are valid:
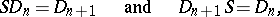 |
where 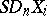 and
and 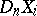 are considered as polyhedra,
are considered as polyhedra, 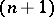 -dual to polyhedra
-dual to polyhedra 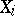 and, correspondingly,
and, correspondingly, 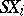 ,
, 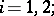 this means that it does not depend on
this means that it does not depend on  and is stationary with respect to suspension.
and is stationary with respect to suspension.
c) It satisfies the equation
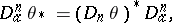 |
where
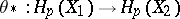 |
and
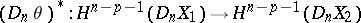 |
are homomorphisms of the above homology and cohomology groups, induced by 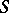 -mappings
-mappings 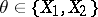 and
and 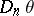 , and
, and
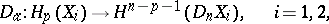 |
is an isomorphism obtained from the isomorphism of Alexander duality by replacing the set 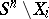 by its
by its 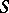 -deformation retract
-deformation retract 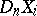 .
.
The construction of 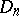 is based on the representation of a given mapping as the composition of an imbedding and an
is based on the representation of a given mapping as the composition of an imbedding and an 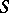 -deformation retract.
-deformation retract.
The 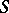 -homotopy group
-homotopy group 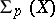 of a space
of a space 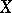 is the group
is the group 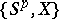 , and the
, and the 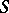 -cohomotopy group
-cohomotopy group 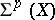 of
of 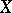 is the group
is the group 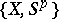 . As in ordinary homotopy theory, one defines the homomorphisms
. As in ordinary homotopy theory, one defines the homomorphisms
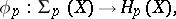 |
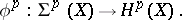 |
Regarding the spheres 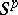 and
and 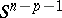 as
as  -dual leads to the isomorphisms
-dual leads to the isomorphisms
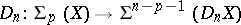 |
and to the commutative diagram
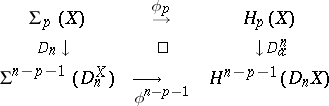 |
Thus, the isomorphism 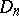 connects
connects 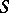 -homotopy and
-homotopy and 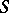 -cohomotopy groups, just as the isomorphism of Alexander duality
-cohomotopy groups, just as the isomorphism of Alexander duality 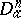 connects the homology and cohomology groups. Any duality in the
connects the homology and cohomology groups. Any duality in the 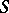 -category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of
-category entails a duality of ordinary homotopy classes if the conditions imposed on the space entail the existence of a one-to-one correspondence between the set of the above classes and the set of 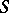 -homotopy classes.
-homotopy classes.
Examples of dual assumptions in this theory include Hurewicz's isomorphism theorem and Hopf's classification theorem. 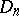 converts one of these theorems into the other, which means that
converts one of these theorems into the other, which means that 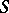 -homotopy groups are replaced by
-homotopy groups are replaced by 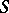 -cohomotopy groups, homology groups by cohomology groups, the mapping
-cohomotopy groups, homology groups by cohomology groups, the mapping 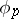 by the mapping
by the mapping 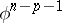 , the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an
, the smallest dimension with a non-trivial homology group by the largest dimension with a non-trivial cohomology group, and vice versa. In ordinary homotopy theory the definition of an  -cohomotopy group requires that the dimension of the space does not exceed
-cohomotopy group requires that the dimension of the space does not exceed 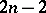 (or, more generally, that the space be
(or, more generally, that the space be 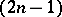 -coconnected,
-coconnected, 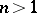 ), which impairs the perfectly general nature of duality.
), which impairs the perfectly general nature of duality.
There are several trends of generalization of the theory: e.g. studies are made of spaces with the 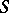 -homotopy type of polyhedra, the relative case, a theory with supports, etc. [3], [5], , [7]. The theory was one of the starting points in the development of stationary homotopy theory [8].
-homotopy type of polyhedra, the relative case, a theory with supports, etc. [3], [5], , [7]. The theory was one of the starting points in the development of stationary homotopy theory [8].
References
| [1] | E.H. Spanier, "Duality and 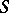 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 -theory" Bull. Amer. Math. Soc. , 62 (1956) pp. 194–203 |
| [2] | E.H. Spanier, J.H.C. Whitehead, "Duality in homotopy theory" Mathematika , 2 : 3 (1955) pp. 56–80 |
| [3] | E.H. Spanier, J.H.C. Whitehead, "Duality in relative homotopy theory" Ann. of Math. , 67 : 2 (1958) pp. 203–238 |
| [4] | M.G. Barratt, "Track groups 1; 2" Proc. London Math. Soc. , 5 (1955) pp. 71–106; 285–329 |
| [5] | E.H. Spanier, J.H.C. Whitehead, "The theory of carriers and 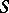 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 -theory" , Algebraic geometry and Topology (A Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 330–360 |
| [6a] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" C.R. Acad. Sci. Paris , 246 : 17 (1958) pp. 2444–2447 |
| [6b] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Suites exactes" C.R. Acad. Sci. Paris , 246 : 18 (1958) pp. 2555–2558 |
| [6c] | B. Eckmann, P.J. Hilton, "Groupes d'homotopie et dualité. Coefficients" C.R. Acad. Sci. Paris , 246 : 21 (1958) pp. 2991–2993 |
| [6d] | B. Eckmann, P.J. Hilton, "Transgression homotopique et cohomologique" C.R. Acad. Sci. Paris , 247 : 6 (1958) pp. 620–623 |
| [6e] | B. Eckmann, P.J. Hilton, "Décomposition homologique d'un polyhèdre simplement connexe" C.R. Acad. Sci. Paris , 248 : 14 (1959) pp. 2054–2056 |
| [7] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [8] | G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) |
S-duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=S-duality&oldid=17724