Theorem prover

automated deduction tool

Software that helps in solving problems and answering questions that involve reasoning. Such assistance comes in two modes: interactive, where one instructs the program to draw some conclusions, present them to the user, and then to ask for a new set of instructions; or fully automatic, where the program is assigned an entire reasoning task.

Automated deduction stands for the automated processing of a variety of reasoning tasks: consequence proving, counterexample generation, model checking, subsumption checking, and satisfiability checking. Application areas of automated deduction include mathematics, program and hardware verification, planning, diagnosis, mathematics and logic education, databases, knowledge representation, and natural language processing.

Some of the main achievements of automated deduction systems include:

proving the Robbins algebra conjecture;

the verification of communications networks too complex for human analysis;

some complete commercial microcontrollers, parts of commercial microprocessors, and their key algorithms have been verified mechanically, although the largest commercial chips are not verifiable using automated deduction tools at present (1998) and probably in the near future;

a number of programming languages are built around deductive methods;

recent (1998) novel uses of automated deduction tools include areas such as economics and sociology; these can profit from the use of (automated) formal methods to express and evaluate theories, for example by testing the consistency of a proposed theory extension and by generating ramifications of a proposed extension.

Theorem-proving tools are built around deduction systems. Resolution-based theorem provers are the most successful ones; the underlying resolution calculus is originally due to J.A. Robinson [a12]. Other, less popular deduction formats for theorem proving are based on the so-called tableaux method (due to E.W. Beth [a3]) and on sequent-based calculi (originally due to G. Gentzen [a4]).

Automated deduction tools are complex pieces of software. The strength of such tools crucially depends on appropriate representation and indexing techniques and memory management. Today's (1998) resolution-based theorem provers explore search spaces of several billion clauses, and advanced model checking software is able to represent complex computational systems with as much as 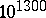many possible states.

Some of the better known provers include Gandalf [a13], Isabelle [a10], NQHTM (also known as the Boyer–Moore theorem prover; [a1]), OTTER [a15], and SPASS [a14]; these are all resolution-based systems. Tableaux-based systems include SETHEO [a8], a well-know sequent-based system is the Logics Workbench LWB [a5], and a well-known model checker is SMV [a9]. There are several specialized journals in the area (see [a6], [a7]) as well as two handbooks (as of 1998) [a2], [a11].

References

[a1]	R.S. Boyer, J.S. Moore, "A computational logic" , Acad. Press (1979)
[a2]	"Automated deduction: A basis for applications" W. Bibel (ed.) P.H. Schmidt (ed.) , Applied Logic Ser. , Kluwer Acad. Publ. (1998)
[a3]	E.W. Beth, "Semantic entailment and formal derivability" Meded. K. Nederl. Akad. Wetensch., Afd. Letterkunde, N.R. , 18 : 13 (1955) pp. 309–342
[a4]	G. Gentzen, "Untersuchungen über das logische Schließen" Math. Z. , 39 (1935) pp. 176–210; 405–431
[a5]	A. Heuerding, "LWB theory: information about some propositional logics via the WWW" J. IGPL , 4 : 4 (1996) pp. 169–174
[a6]	J. Automated Reasoning (0)
[a7]	J. Symbolic Comp. (1)
[a8]	M. Moser, O. Ibens, R. Letz, J. Steinbach, C. Goller, J. Schumann, K. Mayr, "SETHEO and E-SETHEO. The Cade-13 systems" J. Automated Reasoning , 18 : 2 (1997) pp. 237–246
[a9]	K. McMillan, "Symbolic model checking" , Kluwer Acad. Publ. (1993)
[a10]	L.C. Paulson, "Isabelle: a generic theorem prover" , Lecture Notes Computer Sci. , 828 , Springer (1994)
[a11]	"Handbook of Automated Reasoning" J.A. Robinson (ed.) A. Voronkov (ed.) , Elsevier (1999)
[a12]	J.A. Robinson, "A machine-oriented logic based on the resolution principle" J. ACM , 12 (1965) pp. 23–41
[a13]	T. Tammet, "Towards efficient subsumption" , Proc. CADE-15 , Lecture Notes Computer Sci. , 1421 , Springer (1998)
[a14]	C. Weidenbach, B. Gaede, G. Rock, "SPASS & FLOTTER, Version 0.42" , Proc. CADE-13 , Springer (1996)
[a15]	L. Wos, R. Overbeek, E. Lusk, J. Boyle, "Automated reasoning: Introduction and applications" , McGraw-Hill (1992) (Edition: Second)