Extension of a semi-group

A semi-group 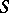containing the given semi-group as a sub-semi-group. One is usually concerned with extensions that are in some way related to the given semi-group . The most well-developed theory is that of ideal extensions (those semi-groups containing as an ideal). To each element of an ideal extension 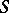of a semi-group 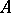are assigned its left and right translations 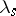, 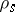: 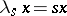, 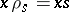(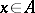); let 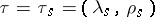. 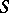The mapping is a homomorphism of into the translation hull 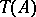of , and is an isomorphism in the case when is weakly reductive (see Translations of semi-groups). The semi-group 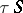is called the type of the ideal extension 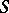. Among the ideal extensions 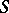of , one can distinguish strong extensions, for which 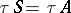, and pure extensions, for which 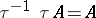. Every ideal extension of is a pure extension of one of its strong extensions.

An ideal extension 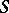of is called dense (or essential) if every homomorphism of 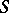that is injective on is an isomorphism. has a maximal dense ideal extension 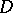if and only if is weakly reductive. In this case, 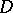is unique up to an isomorphism and is isomorphic to 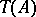. Also, in this case, is called a densely-imbedded ideal in 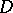. The sub-semi-groups of 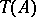containing , and only these, are isomorphic to dense ideal extensions of a weakly reductive semi-group .

If 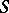is an ideal extension of and if the quotient semi-group 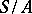is isomorphic to 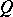, then 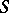is called an extension of 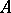by 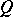. The following cases have been studied extensively: ideal extensions of completely-simple semi-groups, of a group by a completely 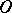-simple semi-group, of a commutative semi-group with cancellation by a group with added zero, etc. In general, the problem of describing all ideal extensions of a semi-group by 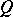is far from being solved.

Among other types of extensions of one can mention semi-groups that have a congruence with 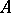as one of its classes, and in particular the so-called Schreier extensions of a semi-group with identity [1], which are analogues of Schreier extensions of groups. In studying the various forms of extensions of a semi-group (in particular, for inverse semi-groups), one uses cohomology of semi-groups.

Another broad area in the theory of extensions of semi-groups is concerned with various problems on the existence of extensions of a semi-group that belong to a given class. Thus, any semi-group can be imbedded in a complete semi-group, in a simple semi-group (relative to congruences), or in a bi-simple semi-group with zero and an identity (see Simple semi-group), and any finite or countable semi-group can be imbedded in a semi-group with two generators. Conditions are known under which a semi-group 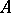can be imbedded in a semi-group without proper left ideals, in an inverse semi-group (cf. Inversion semi-group), in a group (see Imbedding of semi-groups), etc.

References

[1]	A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1 , Amer. Math. Soc. (1961)
[2]	M. Petrich, "Introduction to semigroups" , C.E. Merrill (1973)