Quasi-affine scheme
From Encyclopedia of Mathematics
A scheme isomorphic to an open compact subscheme of an affine scheme. A compact scheme 
is quasi-affine if and only if one of the following equivalent conditions holds: 1) the canonical morphism 
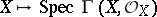is an open imbedding; and 2) any quasi-coherent sheaf of 
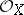-modules is generated by global sections. A morphism of schemes 
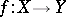is called quasi-affine if for any open affine subscheme 
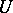in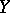 
the inverse image 
is a quasi-affine scheme.
Comments
A quasi-affine variety is an open subvariety of an affine algebraic variety. (As an open subspace of a Noetherian space it is automatically compact.) An example of a quasi-affine variety that is not affine is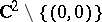 
.
References
| [a1] | A. Grothendieck, "Étude globale élémentaire de quelques classes de morphismes" Publ. Math. IHES , 8 (1961) pp. Sect. 5.1 |
| [a2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 3, 21 |
How to Cite This Entry:
Quasi-affine scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-affine_scheme&oldid=17637
Quasi-affine scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-affine_scheme&oldid=17637
This article was adapted from an original article by V.I. Danilov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article