Monogenic semi-group
cyclic semi-group
A semi-group generated by one element. The monogenic semi-group generated by an element  is usually denoted by
is usually denoted by  (sometimes by
(sometimes by  ) and consists of all powers
) and consists of all powers  with natural exponents. If all these powers are distinct, then
with natural exponents. If all these powers are distinct, then  is isomorphic to the additive semi-group of natural numbers. Otherwise
is isomorphic to the additive semi-group of natural numbers. Otherwise  is finite, and then the number of elements in it is called the order of the semi-group
is finite, and then the number of elements in it is called the order of the semi-group  , and also the order of the element
, and also the order of the element  . If
. If  is infinite, then
is infinite, then  is said to have infinite order. For a finite monogenic semi-group
is said to have infinite order. For a finite monogenic semi-group  there is a smallest number
there is a smallest number  with the property
with the property 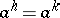 , for some
, for some 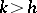 ;
;  is called the index of the element
is called the index of the element  (and also the index of the semi-group
(and also the index of the semi-group  ). In this connection, if
). In this connection, if 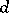 is the smallest number with the property
is the smallest number with the property  , then
, then  is called the period of
is called the period of  (of
(of 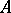 ). The pair
). The pair 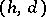 is called the type of
is called the type of  (of
(of 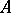 ). For any natural numbers
). For any natural numbers  and
and  there is a monogenic semi-group of type
there is a monogenic semi-group of type 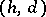 ; two finite monogenic semi-groups are isomorphic if and only if their types coincide. If
; two finite monogenic semi-groups are isomorphic if and only if their types coincide. If  is the type of a monogenic semi-group
is the type of a monogenic semi-group  , then
, then 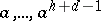 are distinct elements and, consequently, the order of
are distinct elements and, consequently, the order of 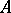 is
is  ; the set
; the set
 |
is the largest subgroup and smallest ideal in 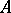 ; the identity
; the identity  of the group
of the group 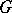 is the unique idempotent in
is the unique idempotent in 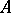 , where
, where 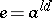 for any
for any  such that
such that 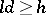 ;
; 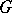 is a cyclic group, a generator being, for example,
is a cyclic group, a generator being, for example, 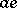 . An idempotent of a monogenic semi-group is a unit (zero) in it if and only if its index (respectively, period) is equal to 1; this is equivalent to the given monogenic semi-group being a group (respectively, a nilpotent semi-group). Every sub-semi-group of the infinite monogenic semi-group is finitely generated.
. An idempotent of a monogenic semi-group is a unit (zero) in it if and only if its index (respectively, period) is equal to 1; this is equivalent to the given monogenic semi-group being a group (respectively, a nilpotent semi-group). Every sub-semi-group of the infinite monogenic semi-group is finitely generated.
References
| [1] | A.H. Clifford, G.B. Preston, "The algebraic theory of semigroups" , 1 , Amer. Math. Soc. (1961) |
| [2] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
Monogenic semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monogenic_semi-group&oldid=17587