Uniform stability

Lyapunov stability, uniform with respect to the initial time. A solution 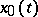, , 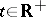of a system of differential equations

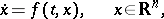is called uniformly stable if for every 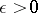there is a 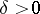such that for every 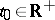and every solution 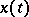of the system satisfying the inequality

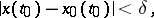the inequality

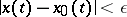holds for all .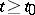

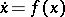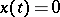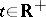A Lyapunov-stable fixed point of an autonomous system of differential equations , , is uniformly stable, but, in general, a Lyapunov-stable solution need not be uniformly stable. For example, the solution , , of the equation

(1)

is stable for each 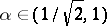but is not uniformly stable for such .

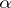Suppose one is given a linear system of differential equations

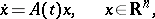(2)

where 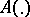is a mapping 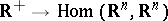that is summable on each interval.

In order that the solution 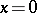of (2) be uniformly stable, it is necessary that the upper singular exponent 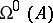of (2) be less than or equal to zero (cf. also Singular exponents). For example, in the case of equation (1), the upper singular exponent 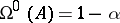, and the Lyapunov characteristic exponent . For the existence of a 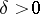such that the solution 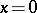of any system

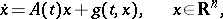that satisfies the conditions of the existence and uniqueness theorem for the solution of the Cauchy problem as well as the condition

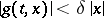be uniformly stable, it is necessary and sufficient that the upper singular exponent 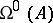be less than zero.

References

[1]	K. Persidskii, "On stability of motion in a first approximation" Mat. Sb. , 40 : 3 (1933) pp. 284–293 (In Russian)
[2]	B.P. Demidovich, "Lectures on the mathematical theory of stability" , Moscow (1967) (In Russian)
[3]	Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian)

Comments

The upper singular exponent is also called the Bohl exponent, cf. also Singular exponents.

References

[a1]	N. Rouché, "Stability theory by Liapunov's direct method" , Springer (1977)
[a2]	J.K. Hale, "Ordinary differential equations" , Wiley (1969)
[a3]	W.A. Coppel, "Stability and asymptotic behavior of differential equations" , D.C. Heath (1965)