Linear system of differential equations with almost-periodic coefficients

A system of ordinary differential equations

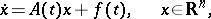(1)

where , 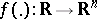are almost-periodic mappings (cf. Almost-periodic function). In coordinate form one has

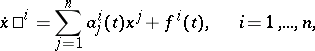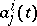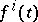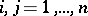where and , , are almost-periodic real-valued functions. Such systems arise in connection with Bohr almost-periodic functions (see [1]). Interest in a narrower class of systems (where 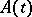and 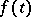are quasi-periodic mappings, cf. Quasi-periodic function) arose much earlier in connection with the examination of variational equations along conditionally-periodic solutions of the equations of celestial mechanics.

If the homogeneous system

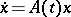(2)

is a system with integral separation (see Integral separation condition), then it reduces to a diagonal system 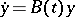with almost-periodic coefficients by an almost-periodic (with respect to 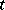) Lyapunov transformation 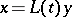; that is, it reduces to a system for which there is a basis of 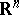, independent of , consisting of vectors that are eigen vectors of the operator 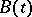for every 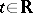. In coordinates with respect to this basis the system 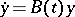is written in diagonal form:

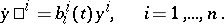The set of systems with integral separation is open in the space of systems (2) with almost-periodic coefficients, endowed with the metric

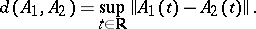The following theorem holds. Let 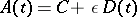, where 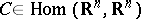, let the eigen values of all be real and distinct, and let 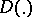be an almost-periodic mapping 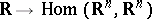. Then there is an 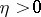such that for all with 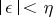the system (2) reduces to a diagonal system with almost-periodic coefficients, by an almost-periodic (with respect to ) Lyapunov transformation.

For an almost-periodic mapping 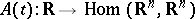the following four assertions are equivalent: 1) for every almost-periodic mapping 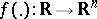there is an almost-periodic solution of the system (1); 2) there is exponential dichotomy of solutions of the system (2); 3) none of the systems 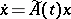, where 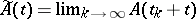, has non-zero bounded solutions; and 4) for every bounded mapping 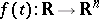there is a bounded solution of the system (1).

References

[1]	H. Bohr, "Almost-periodic functions" , Chelsea, reprint (1947) (Translated from German)
[2]	J. Favard, "Leçons sur les fonctions presque-périodiques" , Gauthier-Villars (1933)
[3]	N.P. Erugin, "Linear systems of ordinary differential equations with periodic and quasi-periodic coefficients" , Acad. Press (1966) (Translated from Russian)
[4]	J.L. Massera, J.J. Shäffer, "Linear differential equations and function spaces" , Acad. Press (1986)
[5]	E. Mukhamadiev, "On invertibility of differential operators in the space of continuous functions bounded on the real axis" Soviet Math. Dokl. , 12 (1971) pp. 49–52 Dokl. Akad. Nauk SSSR , 196 : 1 (1971) pp. 47–49
[6]	Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146

Comments

See also Differential equation, ordinary.

References

[a1]	J.K. Hale, "Ordinary differential equations" , Wiley (1969)