Polyhedral chain
From Encyclopedia of Mathematics
A linear expression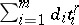 
in a region 
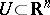, where 
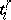are 
-dimensional simplices lying in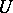 
. By an 
-dimensional simplex (cf. Simplex (abstract)) in 
one means an ordered set of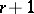 
points in 
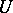whose convex hull lies in 
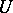. The boundary of a polyhedral chain is defined in the usual way. The concept of a polyhedral chain occupies a position intermediate between those of a simplicial chain of a triangulation of 
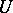and a singular chain in 
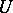, but differs from the latter in the linearity of the simplices.
References
| [1] | P.S. Aleksandrov, "Introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian) |
Comments
The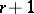 
points making up a simplex are required to be in general position, i.e. they are not all contained in some 
-dimensional affine subspace of 
.
References
| [a1] | L.C. Glaser, "Geometrical combinatorial topology" , 1–2 , v. Nostrand (1970) |
| [a2] | C.R.F. Maunder, "Algebraic topology" , v. Nostrand (1972) |
How to Cite This Entry:
Polyhedral chain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polyhedral_chain&oldid=17498
Polyhedral chain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polyhedral_chain&oldid=17498
This article was adapted from an original article by S.V. Matveev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article