Entire rational function
(algebraic) polynomial
A function of the form
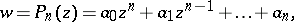 |
where  is a non-negative integer, the coefficients
is a non-negative integer, the coefficients  are real or complex numbers, and
are real or complex numbers, and  is a real or complex variable. If
is a real or complex variable. If 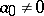 , then
, then  is called the degree of the polynomial; the polynomial
is called the degree of the polynomial; the polynomial 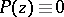 does not have a degree. The simplest non-constant entire rational function is the linear function
does not have a degree. The simplest non-constant entire rational function is the linear function
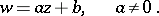 |
An entire rational function is analytic in the whole plane, that is, it is an entire function of the complex variable  , and
, and 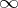 is a pole of order
is a pole of order  for
for 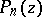 . (
. (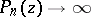 for
for 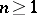 , as
, as 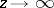 ; conversely, if
; conversely, if 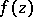 is an entire function and
is an entire function and 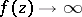 as
as 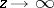 , then
, then 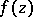 is an entire rational function.) Polynomials in several real or complex variables also play an important role in mathematical analysis. Entire rational functions are used for the approximate representation of more complicated functions because they are most convenient for computations.
is an entire rational function.) Polynomials in several real or complex variables also play an important role in mathematical analysis. Entire rational functions are used for the approximate representation of more complicated functions because they are most convenient for computations.
See also Polynomial.
References
| [1] | I.I. Privalov, "Introduction to the theory of functions of a complex variable" , Moscow (1977) (In Russian) |
Comments
In non-Soviet literature the phrase "entire rational function" is not used.
References
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. 24–26 |
| [a2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
Entire rational function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Entire_rational_function&oldid=17457