Nil flow
From Encyclopedia of Mathematics
A flow on a nil manifold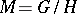 
defined by the action on 
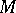of some one-parameter subgroup 
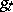of a nilpotent Lie group 
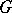: If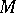 
consists of the cosets 
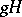, then under the action of the nil flow such a coset at time 
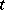goes over in 
.
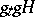References
| [1] | L. Auslander, L. Green, F. Hahn, "Flows on homogeneous spaces" , Princeton Univ. Press (1963) |
Comments
The first example of a compact minimal flow that is distal but not equicontinuous was a nil flow (cf. Distal dynamical system; Equicontinuity).
How to Cite This Entry:
Nil flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nil_flow&oldid=17406
Nil flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nil_flow&oldid=17406
This article was adapted from an original article by D.V. Anosov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article