Faber polynomials
A classical basis system that serves to represent analytic functions in a complex domain. Suppose that the complement of a bounded continuum 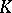 containing more than one point is a simply-connected domain
containing more than one point is a simply-connected domain 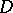 of the extended complex plane
of the extended complex plane 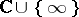 , and that the function
, and that the function  ,
, 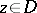 , is the conformal univalent mapping of
, is the conformal univalent mapping of 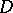 onto the domain
onto the domain  under the conditions
under the conditions 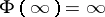 and
and 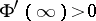 . Then the Faber polynomials
. Then the Faber polynomials  can be defined as the sums of the terms of non-negative degree in
can be defined as the sums of the terms of non-negative degree in  in the Laurent expansions of the functions
in the Laurent expansions of the functions 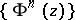 in a neighbourhood of the point
in a neighbourhood of the point 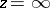 . The Faber polynomials for
. The Faber polynomials for 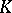 can also be defined as the coefficients in the expansion
can also be defined as the coefficients in the expansion
 | (1) |
where the function 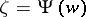 is the inverse of
is the inverse of 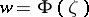 . If
. If 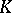 is the disc
is the disc 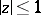 , then
, then 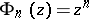 . In the case when
. In the case when 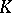 is the segment
is the segment 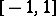 , the Faber polynomials are the Chebyshev polynomials of the first kind. These polynomials were introduced by G. Faber [1].
, the Faber polynomials are the Chebyshev polynomials of the first kind. These polynomials were introduced by G. Faber [1].
If 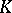 is the closure of a simply-connected domain
is the closure of a simply-connected domain  bounded by a rectifiable Jordan curve
bounded by a rectifiable Jordan curve 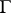 , and the function
, and the function 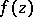 is analytic in
is analytic in  , continuous in the closed domain
, continuous in the closed domain 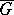 and has bounded variation on
and has bounded variation on 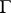 , then it can be expanded in
, then it can be expanded in 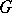 in a Faber series
in a Faber series
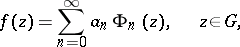 | (2) |
that converges uniformly inside  , that is, on every closed subset of
, that is, on every closed subset of  , where the coefficients in the expansion are defined by the formula
, where the coefficients in the expansion are defined by the formula
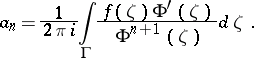 |
The Faber series (2) converges uniformly in the closed domain 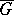 if, for example,
if, for example, 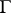 has a continuously-turning tangent the angle of inclination to the real axis of which, as a function of the arc length, satisfies a Lipschitz condition. Under the same condition on
has a continuously-turning tangent the angle of inclination to the real axis of which, as a function of the arc length, satisfies a Lipschitz condition. Under the same condition on 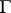 , the Lebesgue inequality
, the Lebesgue inequality
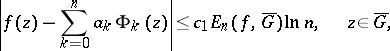 |
holds for every function 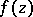 that is analytic in
that is analytic in  and continuous in
and continuous in 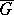 , where the constant
, where the constant 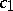 is independent of
is independent of  and
and  , and
, and 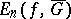 is the best uniform approximation to
is the best uniform approximation to 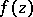 in
in 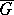 by polynomials of degree not exceeding
by polynomials of degree not exceeding  .
.
One can introduce a weight function 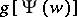 in the numerator of the left-hand side of (1), where
in the numerator of the left-hand side of (1), where 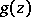 is analytic in
is analytic in 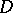 , is different from zero and
, is different from zero and 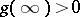 . Then the coefficients of the expansion (1) are called generalized Faber polynomials.
. Then the coefficients of the expansion (1) are called generalized Faber polynomials.
References
| [1] | G. Faber, "Ueber polynomische Entwicklungen" Math. Ann. , 57 (1903) pp. 389–408 |
| [2] | P.K. Suetin, "Series in Faber polynomials and several generalizations" J. Soviet Math. , 5 (1976) pp. 502–551 Itogi Nauk. i Tekhn. Sovr. Probl. Mat. , 5 (1975) pp. 73–140 |
| [3] | P.K. Suetin, "Series in Faber polynomials" , Moscow (1984) (In Russian) |
Comments
[a1] is a general reference concerning approximation of functions of a complex variable. It contains a section on Faber expansions.
References
| [a1] | D. Gaier, "Vorlesungen über Approximation im Komplexen" , Birkhäuser (1980) |
| [a2] | J.H. Curtiss, "Faber polynomials and Faber series" Amer. Math. Monthly , 78 (1971) pp. 577–596 |
| [a3] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) pp. Chapt. 3.14 (Translated from Russian) |
Faber polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Faber_polynomials&oldid=17377