Cartan decomposition

A representation of a real non-compact semi-simple Lie algebra (cf. Lie algebra, semi-simple) as a direct sum of vector spaces (*). If denotes the complexification (complex envelope) of (cf. Complexification of a Lie algebra), then there exists in a real compact subalgebra of the same dimension as such that the following decompositions into direct sums of vector spaces hold:

(*)

where 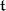is the subalgebra of invariant elements of some involutory automorphism (involution) of and 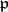is the set of anti-invariant elements of 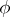. The second formula is the Cartan decomposition of (see [1]). The Cartan decomposition reduces the classification of real non-compact semi-simple Lie algebras to that of compact semi-simple Lie algebras and involutory automorphisms in them.

References

[1]	S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962)