Dvoretzky problem

for random covering

Roughly speaking, random covering is the (attempt at) covering a given large body by means of smaller bodies that are randomly distributed.

There is a large amount of literature on random covering. See [a1] for a general approach; [a3] for the fractal aspect; [a11] for the special case of small convex bodies of given shape and size.

The Dvoretzky problem is about the circle 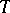of length 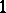and random intervals on it whose lengths 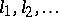are given (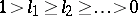), and whose positions on 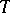are randomly distributed in the usual way. A century ago, E. Borel already knew that when 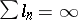, any given point of 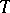is covered almost surely. In 1956, A. Dvoretzky observed that this does not imply that the whole circle is covered almost surely [a5]. When 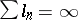, the uncovered set has Lebesgue measure zero almost surely. Is it possible to be more precise? Is it possible to get good necessary and sufficient conditions for covering? Is it possible to do the same in several dimensions?

To apply the zero-one law (i.e., the probability is either zero or one), it is slightly more convenient to consider infinite coverings, meaning that each point is covered by infinitely many intervals.

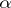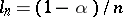After Dvoretzky, the first important systematic study was made by P. Billard [a4] (see Billard method). Using Billard's method, J.-P. Kahane was able to compute the Hausdorff dimension of the uncovered set; for example, this dimension is if [a2]. More precise results, involving capacity with respect to a kernel constructed from 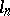, have been obtained later, in [a13].

A most spectacular result was obtained by L. Shepp in 1972 [a15]: covering holds if and only if the series

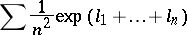diverges; for example, covering holds when .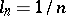

The problem was subsequently extended in several ways.

B. Mandelbrot has considered a similar problem on the line, with random cutouts associated with a Poisson measure in a half-plane, and discovered the relation between the uncovered set and the range of the Lévy process [a14]; this programme was completed by P. Fitzsimmons, B. Fristedt and Shepp in 1985 (see Fitzsimmons–Fristedt–Shepp theorem, [a9]). In this context, the covering condition was established already by Shepp in 1972 [a16].

M. Wschebor considered coverings or cutouts by random sets, not necessarily intervals. His result: When the measures are given, the best covering is realized by intervals [a17], [a18].

J. Hoffmann-Jørgensen has put forth a general framework: random balls in a metric space [a10]. Y. El Hélou was able to compute the Hausdorff dimension of the uncovered set when random balls of given volumes 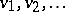are placed on a 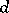-dimensional torus [a2]. Fan Ai-hua has given a necessary and sufficient condition for the covering of a given subset of an ultrametric space, a natural question in percolation on trees [a7].

The Dvoretzky problem for random balls of given volumes on the torus 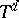is still unsolved. However, there is a natural guess for the necessary and sufficient condition, and the problem for homothetic simplices has been completely solved by Kahane [a13] (see Billard method).

Another generalization of the Dvoretzky problem: instead of the lengths 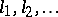, suppose one is given positive functions 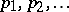on 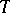. Consider the series of random translates

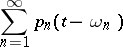(with 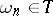independent and Lebesgue distributed). One now asks for the probability that it diverges everywhere. The Dvoretzky problem corresponds to 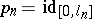. The case with 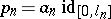is investigated in [a8]; the general case needs new ideas.

References

[a1]	D. Hall, "Introduction to the theory of coverage processes" , Wiley (1988)
[a2]	J.-P. Kahane, "Some random series of functions" , Cambridge Univ. Press (1985) (Edition: Second)
[a3]	B.B. Mandelbrot, "The fractal geometry of nature" , Freeman (1982)
[a4]	P. Billard, "Séries de Fourier aléatoirement bornées, continues, uniformement convergentes" Ann. Sci. Ecole Norm. Sup. , 82 (1965) pp. 131–179
[a5]	A. Dvoretzky, "On covering a circle by randomply placed arcs" Proc. Nat. Acad. Sci. USA , 42 (1956) pp. 199–203
[a6]	Y. El Hélou, "Recouvrement du tore 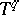par des ouverts aléatoires er dimension de Hausdorff de l'ensemble non recouvert" C.R. Acad. Sci. Paris , 287A (1978) pp. 815–818
[a7]	A.-h. Fan, "Sur quelques processus de naissance et de mort" C.R. Acad. Sci. Paris , 310 (1990) pp. 441–444
[a8]	A.-h. Fan, J.-P. Kahane, "Rareté des intervalles recouvrant un point dans un recouvrement aléatoire" Ann. Inst. H. Poincaré , 20 : 3 (1993) pp. 453–466
[a9]	P.J. Fitzsimons, B. Fristedt, L.R. Shepp, "The set of real numbers left uncovered by random covering intervals" Z. Wahrscheinlichkeitsth. verw. Gebiete , 70 (1985) pp. 175–189
[a10]	J. Hoffmann-Jørgensen, "Coverings of metric spaces with randomly placed balls" Math. Scand. , 32 (1973) pp. 179–186
[a11]	S. Janson, "Random covering in several dimensions" Acta Math. , 156 (1986) pp. 83–118
[a12]	J.-P. Kahane, "Sur le recouvrement d'un cercle par des arcs disposés au hasard" C.R. Acad. Sci. Paris , 248 (1959) pp. 184–186
[a13]	J.-P. Kahane, "Recouvrements aléatoires et théorie du potentiel" Coll. Math. , 60/1 (1990) pp. 387–411
[a14]	B.B. Mandelbrot, "Renewal sets and random cutouts" Z. Wahrscheinlichkeitsth. verw. Gebiete , 22 (1972) pp. 145–157
[a15]	L.A. Shepp, "Covering the circle with random arcs" Israel J. Math. , 11 (1972) pp. 328–345
[a16]	L.A. Shepp, "Covering the line by random intervals" Z. Wahrscheinlichkeitsth. verw. Gebiete , 23 (1972) pp. 163–170
[a17]	M. Wschebor, "Sur le recouvrement du cercle par des ensembles placés au hasard" Israel J. Math. , 15 (1973) pp. 1–11
[a18]	M. Wschebor, "Sur un théorème de L. Shepp" Z. Wahrscheinlichkeitsth. verw. Gebiete , 27 (1973) pp. 179–184