Adjoint space
From Encyclopedia of Mathematics
of a topological vector space 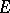
The vector space 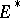 consisting of continuous linear functions on
consisting of continuous linear functions on 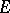 . If
. If 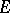 is a locally convex space, then the functionals
is a locally convex space, then the functionals 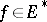 separate the points of
separate the points of 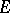 (the Hahn–Banach theorem). If
(the Hahn–Banach theorem). If 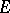 is a normed space, then
is a normed space, then 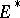 is a Banach space with respect to the norm
is a Banach space with respect to the norm
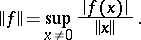 |
There are two (usually different) natural topologies on 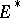 which are often used: the strong topology determined by this norm and the weak-
which are often used: the strong topology determined by this norm and the weak- -topology.
-topology.
References
| [1] | D.A. Raikov, "Vector spaces" , Noordhoff (1965) (Translated from Russian) |
Comments
Instead of the term adjoint space one more often uses the term dual space. The weak- -topology on
-topology on 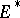 is the weakest topology on
is the weakest topology on 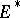 for which all the evaluation mappings
for which all the evaluation mappings 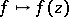 ,
, 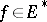 ,
, 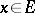 , are continuous.
, are continuous.
References
| [a1] | H.H. Schaefer, "Topological vector spaces" , Macmillan (1966) |
How to Cite This Entry:
Adjoint space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_space&oldid=17289
Adjoint space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_space&oldid=17289